Difference between revisions of "Projects:2018s1-192 Karplus-Strong Synthesis of Sound"
(→Results) |
(→Signal Analysis) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 140: | Line 140: | ||
==Results== | ==Results== | ||
| − | Signal Analysis | + | ===Signal Analysis=== |
| − | + | Matlab was used to analyse signals from both synthesiser, to determine the harmonic content present in a particular note recorded and how these harmonics behaved over time. | |
Digital Signal | Digital Signal | ||
| Line 153: | Line 153: | ||
The frequencies in the analogue signal do not necessarily decay faster the higher the frequency (as is the case with the digital signal), instead the pattern is more irregular, which again is something seen in real instruments and may be due to resonance. | The frequencies in the analogue signal do not necessarily decay faster the higher the frequency (as is the case with the digital signal), instead the pattern is more irregular, which again is something seen in real instruments and may be due to resonance. | ||
| + | Analogue Signal Spectrogram | ||
| − | [[File:Spec10kHzA1a.png | | + | [[File:Spec10kHzA1a.png | 500px]] |
| − | |||
| + | Digital Signal Spectrogram | ||
| − | Subjective Analysis | + | [[File:Spec10kHzA1d.png | 500px]] |
| + | |||
| + | ===Subjective Analysis=== | ||
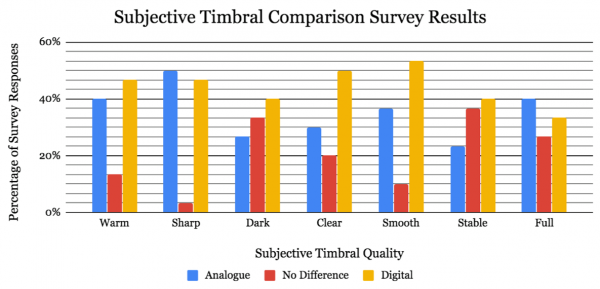
Individuals where asked to compare signals generated from both the analogue and digital synthesiser and provide an answer as to which signal sounded more like a particular tonal characteristic, or if no difference was perceived. The results can be seen as a bar graph. The surveys results show that opinion was divided for a number of qualities, which means that the two synthesis methods do differ tonally and produce different sounds. | Individuals where asked to compare signals generated from both the analogue and digital synthesiser and provide an answer as to which signal sounded more like a particular tonal characteristic, or if no difference was perceived. The results can be seen as a bar graph. The surveys results show that opinion was divided for a number of qualities, which means that the two synthesis methods do differ tonally and produce different sounds. | ||
Latest revision as of 14:41, 19 October 2018
Contents
Project Team
- David McQueen
- Samuel Churches
- Sam Haberman
Supervisors
- Dr Andrew Allison
- Dr Brian Ng
Introduction
The Karplus-Strong (KS) plucked-string algorithm was a computational model developed in the early 1980s as an efficient model for vibrating strings based on physical resonance. It was praised for the rich and realistic timbres it generated despite its simplicity. Briefly explained, the algorithm works by placing a delay element into a positive feedback configuration together with a simple low pass filter. Short noise bursts injected into the feedback loop will resonate in the system at a frequency defined by the delay period, and decay away due to the action of the filter. This model is analogous to a plucked string, with the noise bursts acting as the plucks, and the resonating feedback loop acting as the string medium. By modifying the transient shape and frequency content of the noise burst, and the cutoff frequency and gain of the filter, different pleasing output timbres can be synthesised.
Since its conception, many advances have been made in developing the KS algorithm in efforts to generate more realistic models of instruments and to widen the range of instruments available for simulation through advances in the theory of digital waveguides for the modelling of multi-dimensional systems. Efforts have been made to produce musical synthesisers as products, with patents being applied for in 1986 and 1987 and both Mattel and Yamaha licensing the technology however no products have been brought to market using the algorithm from these efforts.
Some modular synthesiser systems are available that provide sufficient building blocks to run a Karplus-Strong model, but these synthesisers are cumbersome, do not support easy chromatic tuning and require much work to implement polyphony, and as such lack playability via standard MIDI control methods.
Abstract
The goal of the project is to develop two synthesizers based on the Karplus-Strong algorithm. The first will implement the model using analog electronics, with digital electronics to control it and the second will be purely digitally based. The synthesizers will be required to be playable using a MIDI controller (such as a keyboard) and have a user interface that allows the character of the generated music to be intuitively adjusted.
The three main research goals of this project are to:
- Highlight the frequency domain differences between Karplus-Strong synthesisers implemented in the digital domain and with analogue electronics
- Study the subjective perceptual timbral differences between analogue and digital Karplus-Strong synthesisers through systematic surveying
- Investigate the commercial viability of producing a hardware Karplus-Strong synthesiser using analogue electronics.
The basis of the analogue electronics KS implementation are bucket-brigade delay lines, and the digital synthesiser is implemented in the MATLAB environment.
Background
Karplus-Strong Synthesis
Karplus-Strong (KS) synthesis produces musical notes by impulsing a filtered positive feed- back delay line with short bursts of noise. The method was presented in 1983 as a way to digitally synthesise musical notes using as little computational overhead as possible. KS synthesis works as a simplified physical model of a plucked string, such as that found on a guitar, cello or harp. The noise burst represents the energy stimulation (pluck) imparted on the string. The delay element encapsulates the time delay between the energy wave on the string, as a result of stimulation, travelling between each reflective ends of the string. The low pass filter attenuates high frequency components in the ’reflected’ wave (delayed impulse), imitating the same dampening effect found in real plucked strings due to viscosity in the air medium they travel on, and the energy transferred to the reflective element. Gain control in the feedback path regulates the sustain effect of a plucked string, with a lower feedback gain leading to a shorter note sustain time. Gain control is limited to unity, or below, such that the output signal will always decay to zero. Finally, the summing element of the feedback loop adds the reflected waves back into the signal path, to be delayed and filtered again.
By tuning the delay period to be that of the frequency of a desired note, and using appropriate filtering and gain parameters, the Karplus-Strong model can synthesise realistic plucked string timbres.
Bucket-Brigade Devices
Bucket-brigade devices (BBD) are discrete time, continuous voltage analogue signal delay lines. They function as a queue of electrical charges stored in capacitors, shifted along by switching MOSFETs using alternating clock signals. The high price of bucket brigade devices is the past was prohibitive of their use in affordable synthesisers, but now these devices are affordable, which has encouraged their use in this project. Additionally, to precisely control the delay line, a highly precise digitally controlled clock signal is required, the implementation of which has only become cost effective for use in synthesis in recent years.
Transient Envelopes
A common control signal used in synthesisers is called an envelope. An envelope is triggered by note a gate and/or a trigger signal, which are engaged by a new keyboard note event, and outputs a control voltage which will typically control either a filter cutoff frequency or the gain of a note output signal. An typical envelope has four control parameters: attack, sustain, decay and release (ADSR). Attack controls the time from the start of the note event to the envelope reaching its peak level. Decay controls the time from the envelope reaching its peak level to reaching its sustain point. Sustain controls the level of the sustain point. Release controls the time from the note gate ending to the envelope reaching zero.
Market Analysis
Analogue electronics based instruments and effects units are currently seeing a renaissance in the music technology market. Consumers are returning to older music technology, embracing their subtle imperfections and rich tonality compared to their digital counterparts, which are perceived as comparatively sterile [5]. Karplus-Strong synthesis is also receiving more attention in recent times, as the computational power required for detailed, polyphonic, real time KS synthesis becomes cheaper and more readily available.
At this point in time, no fully integrated KS synthesiser implemented using analogue electronics exists. It is predicted that due to the current state of the market, there may be a consumer demand for this product. The function of this project is to determine whether such an analogue implementation is different enough to warrant bringing this product to market.
Method
Analogue Synthesiser Design
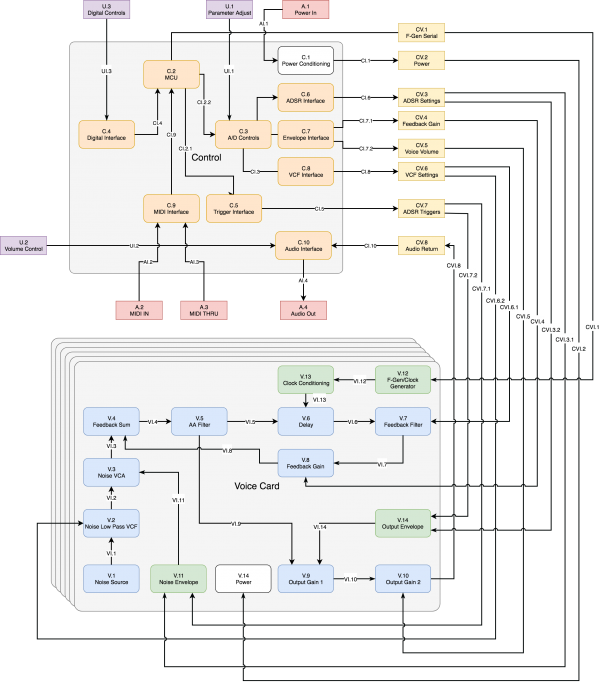
A high level design outlining all major subsystems in the analogue KS synthesiser is presented below.
Bucket Brigade Delay
The first BBD that was investigated was the 512 stage Phillips TDA1022. It was chosen as an ideal candidate for its comparatively wide range of delay periods (51.2 - 0.512ms) compared to other BBDs, which would allow a wide range of playable note frequencies (19.5Hz - 1953.1Hz). The TDA1022 has ceased production, and because of this is quite difficult to attain. However, due to the bespoke nature of this instrument prototype, it was deemed within the project’s budget to use the TDA1022.
A batch of ten TDA1022 DIP-16 packages were procured via an online eBay auction, with a price of approximately $8 each. After extensive attempts using all ten units in both manufacturer test circuits, and third party delay line circuit designs, none of these BBDs were able to function correctly. It is believed that the ICs were either counterfeits, factory discarded units, or have degraded over time due to high temperature storage. Prices for the TDA1022 from other vendors are well in excess of $20 each, which is too expensive for this project, and is not a cost or risk that was deemed worthwhile.
The next BBD to be assessed for implementation was the CoolAudio V3207. This IC, currently being mass manufactured, is a reproduction of the 1024 stage MN3207 BBD manufactured by Panasonic in the mid 1970’s. While having a more limited and slower delay range (2.56-51.2ms) than the TDA1022, it is easily procured new and is of significantly lower cost per unit (∼ $2).
Clock Conditioning
The output of the function generator (V.12) is defined by interface VI.12, which states that it will be a square wave with logic levels VOH = 3.3V, and VOL = 0V. To condition this signal such that it is suitable for a BBD clock input, it must be converted into two antiphase clock signals, and their logic levels must be raised to the prescribed levels of the BBD.
The first BBD investigated, the Phillips TDA1022, required a clock signal VIH =−1.5↔0V, and VIL = −10 ↔ −18V= −15V (typical). To attain the large logic level shift and antiphase copy required, inputting the clock signal into an inverting, and non-inverting op- amp (Operational Amplifier) Schmitt trigger design was tested. For this method, the initial logic level shift of the function generator clock signal from 0 ↔ 3.3V to 0 ↔ −3.3V required to trigger the Schmitt triggers was to be determined later. Using a function generator to output a 0 ↔ −3.3V clock signal, the output of each Schmitt trigger was analysed using a digital oscilloscope. Initial testing with common op-amp IC’s (LM741, TL07X) showed that for such a big voltage swing (0 ↔ −15V), the op-amp slew rate caused significant reduction in the output logic rise and fall time.
Op-amps with this relatively high slew rate were found to be particularly expensive, to the point that this method was no longer cost effective. Thus, the op-amp Schmitt trigger method of clock conditioning was abandoned.
Next, a variation of the Schmitt trigger method was attempted, using the 40106 hex Schmitt trigger inverter IC. This 14 pin DIP IC contains 6 fully integrated, high performance inverting Schmitt triggers, and can operate at the voltage swing level required for the TDA1022. By feeding the digital clock signal into one Schmitt trigger inverter, and then feeding the output of that into another Schmitt trigger inverter, the outputs of the two Schmitt trigger inverters were the required antiphase clock signals. One caveat of this method was that the VIH threshold of the 40106 was greater than the 3.3V that the digital clock function generator could output. It was proposed that the function generator (FG) would output a sine wave, which would be amplified to a level that it would trigger a 50% duty cycle clock output from the Schmitt trigger IC. Simulating these conditions with a bench function generator, an acceptable set of clock signals were generated, but due to the malfunctioning TDA1022 IC’s, the credibility of these signals was unable to verified.
Despite the op-amp Schmitt trigger design being able to meet this slew specification with medium cost op-amps, it was found to be more cost effective to use Schmitt trigger ICs.
Because of the lower clock voltage level requirements of the V3207 BBD, a different Schmitt trigger IC can be used. The 74HC14 hex Schmitt trigger offers incredibly fast logic rise and fall times (effectively instantaneous for the required clock speeds), and robust output buffering. This is desirable, as it may allow for overclocking of the BBD delay times.
Voltage Controlled Low Pass Filters
The first VCF designed and tested was the Bridged-T filter. The component values used in the final design, were chosen based on Hendrik Göttling’s Bridged-T filter implementation with some minor alterations. The bypass capacitor on the output was removed to better study the output interface, and the variable resistor in the bridge network was replaced with a resistor chosen to minimise resonance at the cutoff frequency. The value of the resistor was chosen with respect experimental and simulated results.
This design was favoured initially for its simplicity and low cost. Unfortunately, the Bridged- T VCF design was not able to be used for a variety of reasons. First, this type of active filter is naturally very resonant. Despite much experimentation with component values, both in a simulation environment and using real circuits, there was an unavoidable peak in gain resonating at the cutoff frequency. This was incompatible with the KS loop because it is in the signal path of a positive feedback loop. In a positive feedback loop resonant frequencies will be amplified, and will limit the feedback gain to be extremely low for the system to remain stable. The other reason for the rejection of this filter design was the fact that it was acting as an inverting amplifier. Many attempts were made to adapt this design to a non-inverting structure, but due to the less than intuitive function of this filter, no functioning non-inverting designs were successfully made. While this could be easily alleviated by using an inverting op-amp buffer, this would somewhat negate the cost reduction from this filter design. Therefore, the Bridged-T VCF design was ultimately discarded, and no further measurements were made.
The next filter design was a 2nd order Butterworth low-pass VCF using two buffered OTA’s, specifically those on the LM13700 integrated OTA package. The design, was taken directly from an example design in the TI datasheet, and upon construction, initial testing of the filter’s response was promising. Please note that the two darlington pair buffers are contained within the IC. From here, frequency magnitude and delay responses of the filter were taken at various cutoff control voltage (CV) levels.
Anti-Aliasing and Reconstruction Filter
The AA filter design has several requirements which all must be taken into consideration. These are to allow a satisfactory note range of the KS synthesiser, satisfy the Nyquist criteria, attenuate clocking noise, have little resonant feedback at the cutoff frequency (as this it is in a positive feedback loop), and have a suitable cutoff frequency to retain desirable upper harmonics.
Allowing a satisfactory frequency range for the KS synthesiser means that the stopband (20dB attenuation) frequency W of the AA filter, at which the Nyquist criteria fs ≥ 2W is satisfied, must allow for a sufficiently low minimum note frequency. In keeping with the idea of physically modelling acoustic instruments, the target for a ’sufficiently low minimum note frequency’ is approximately 82.4Hz, as this is the frequency of the lowest note produced by an acoustic guitar. Therefore, the stopband frequency of the AA filter should be sufficiently low to accommodate this requirement.
Retaining upper harmonics is also important to the KS synthesiser, as the frequency content of the synthesised outputs in the higher frequency bands (10kHz-20kHz) contribute to its desirable timbral complexity. Additionally, having a stopband frequency that is too low will lead to notes in the high frequency range being significantly more dampened than those in the low frequency range. Therefore, the stopband frequency of the AA filter should be sufficiently high not to attenuate desirable upper harmonics.
Consequently, there are conflicting upper and lower bounds on the cutoff frequency require- ments, and therefore compromise in the design will be needed.
To make an adequate compromise to satisfy these requirements, careful filter design was be needed. First, a four pole, active Butterworth filter topology was chosen for this design for its steep -24db/octave monotonic frequency rolloff (which will not significantly modify the instrument’s timbre), low resonance, and low cost design. After much experimentation done by hand, moving the -24db/octave frequency magnitude response across a Bode plot, a cutoff frequency was chosen which made a compromise between the two conflicting de- sign requirements. Choosing cutoff frequency fc = 18kHz gives a stop band frequency of approximately fstopband = 26kHz using a fourth order low pass filter, which in turn gives a minimum sampling frequency of fs ≥ 52kHz, and therefore a minimum note frequency of 99.6Hz. This was chosen as it balances the passing of high frequency content, only attenuating frequencies ranging 18-20kHz, and also allows for a minimum frequency only two semitones higher than the desired minimum of 82.4Hz. Frequencies lower than 99.6Hz are still possible, but the system will likely impart aliasing artefacts on the output signal. Designing the components of a four-pole active Butterworth filter was achieved, for the sake of convenience, using an automated filter design and simulation tool from Texas Instruments. Reviewing the simulated Bode plot gave preliminary confirmation that this filter satisfies the design requirements, having minimal resonance, and correct cutoff and stopband frequencies. having minimal resonance, and correct cutoff and stopband frequencies.
Feedback Gain and Sum
The function of the feedback sum is to add the input noise impulse signal to the delayed feedback signal, and output this sum to the KS loop, to create a positive feedback loop. A non-inverting summing op-amp configuration was chosen for the feedback sum implementation. The electronic implementation of this is trivial, with equally sized resistors used on each input signal path for equal summing factors.
The feedback gain has the requirement of being user controlled, such that the sustain time of each synthesised note can be controlled. This function was chosen to be implemented using a CoolAudio V2164 Quad Voltage Controlled Amplifier (VCA). This integrated circuit contains four VCAs, which is enough for all of the voltage controlled amplification functions on a single KS synth voice card. The VCA implementation will use the manufacturer defined circuit design, with TL074 op-amps instead of those defined in the aforementioned design. The generation and control of the CV signals are outside the scope of this report.
Output Stage EG & VCA
The envelope generation for the KS synthesiser was chosen to be performed by an ALFA RPAR AS3310 integrated circuit. This fully contained envelope generator (EG) is a contemporary reproduction of a Curtis Electromusic Specialities IC, the CEM3310, most famously used in 1980’s polyphonic synthesisers such as the Oberheim OB-X and the Sequential Prophet 5. The AS3310 provides voltage control of its ADSR (Attack, Sustain, Decay, and Release) parameters, and outputs the resulting envelope as a control voltage in response to a gate signal. This envelope is triggered by a gate control voltage signal generated by each new MIDI event, and controls the gain of a VCA on the output signal path of each voice card. The implementation of the envelope generator will follow the manufacturer’s designed circuit, which only requires externally generated input control voltages and some passive components.
The VCA implementation was identical to that used earlier in the project.
System Evaluation
The implementation of the KS loop system into the KS synthesiser will be described in this section. It is planned that the KS loop will be implemented on a custom PCB using surface mount components, alongside the noise impulse generation system. Therefore, close integration work will be needed to ensure these systems function correctly on the same PCB.
Results
Signal Analysis
Matlab was used to analyse signals from both synthesiser, to determine the harmonic content present in a particular note recorded and how these harmonics behaved over time.
Digital Signal
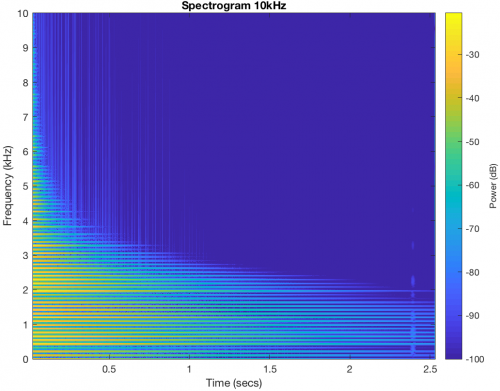
The signals from the digital Karplus-Strong synthesiser showed cleaner spectrums in the FFT and STFT plots. This means that there was little noise present in the signal. There was still a high amount of harmonic content, but these were limited to the expected frequencies due to the comb filtering introduced by the delay. The fundamental frequencies decay exponentially with a very definite slope and very little deviation. The peaks in the FFT are purely the fundamental and harmonic frequencies expected, so there were no unwanted or extra harmonics present in the signal, this is also as expected due to the nature of the digital synthesis.
Analogue Signal
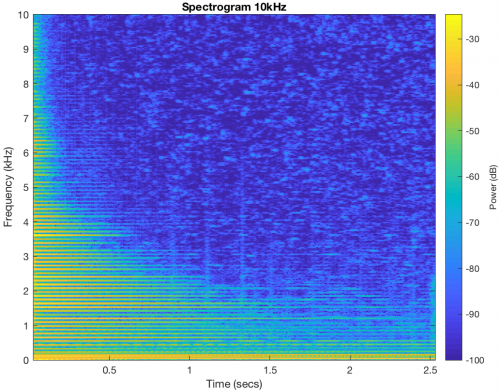
When compared to the digital signal, the analogue signal has much more noise present, over the entire frequency range. The FFT shows a significant 50Hz and 150Hz component present in the recorded signals, this is due to interference from mains AC power, which is not present in the digital signal. The fundamental and harmonics still decay exponentially with time, but there are oscillations in the signal, which will change the character of the produced sounds. This is more like a real instrument, although not to the same degree. The frequencies in the analogue signal do not necessarily decay faster the higher the frequency (as is the case with the digital signal), instead the pattern is more irregular, which again is something seen in real instruments and may be due to resonance.
Analogue Signal Spectrogram
Digital Signal Spectrogram
Subjective Analysis
Individuals where asked to compare signals generated from both the analogue and digital synthesiser and provide an answer as to which signal sounded more like a particular tonal characteristic, or if no difference was perceived. The results can be seen as a bar graph. The surveys results show that opinion was divided for a number of qualities, which means that the two synthesis methods do differ tonally and produce different sounds.
Conclusions and Future Work
In conclusion, the design and research conducted for this project presents multiple outcomes. First, it has shown that implementation of the subsystems of a KS synthesiser is possible using analogue electronics, but the efficacy of these subsystems as a full KS synthesiser has yet to be determined. Digital KS synthesis has been achieved successfully, and a method for modelling the filters used in the analogue synthesiser has been proposed. The motivations for creating an analogue KS synthesiser have been discussed, and comparative mechanisms for evaluating its value to the music technology market have been presented. Whilst there are differences tonally between the digital and analogue synthesisers, no conclusion can be drawn regarding the merit of a KS synthesiser implemented with analogue electronics as yet.
Alternative implementations of KS synthesis could be studied further in the interest of creating unique and desirable musical instruments for the music technology market. Investigations into alternative methods of creating variable signal delay lines, such as physically separated transducers, could be valuable, as the BBD delay line is still a discrete time device. Further study could also be done on modelling the phase delay of analogue electronic filters and amplifiers, to aid in the tuning of analogue KS synthesisers.