Difference between revisions of "Projects:2016s1-121 Measurement of Transformer Parameters"
(→Method of Least Square for Phasors) |
|||
| Line 35: | Line 35: | ||
==''Method of Least Square for Phasors''== | ==''Method of Least Square for Phasors''== | ||
| − | Applying the fourier series theory [3] for a periodic function , having frequency of ω and N sample data, it can be represented as an infinite sum of cosine and sine terms of descrete frequency of integer multiple of ω. | + | Applying the fourier series theory [3] for a periodic function , having frequency of ω and N sample data, it can be represented as an infinite sum of cosine and sine terms of descrete frequency of integer multiple of ω. |
| + | [[File:Untitled.png]] | ||
| + | |||
=='''Previous Study'''== | =='''Previous Study'''== | ||
The previous project, “Estimation and Measurement of Transformer Parameters” has been taken as the basic input for our project. Developing Matlab code for least Square Spectral Analysis performed on the measured voltage and current values, applying T-parameters used to estimate the seven transformer parameters under linear condition, and developing non-linear model of transformer are the other aims of the project. | The previous project, “Estimation and Measurement of Transformer Parameters” has been taken as the basic input for our project. Developing Matlab code for least Square Spectral Analysis performed on the measured voltage and current values, applying T-parameters used to estimate the seven transformer parameters under linear condition, and developing non-linear model of transformer are the other aims of the project. | ||
Revision as of 15:03, 26 October 2016
Contents
Project Title
Measurement of Transformer Parameters
Student Name
Chen Qiao Rahel Bekele Megersa
Supervisors
Dr. Andrew Alison Dr. Rastko Zivanovic
Abstract
This project is identifying a semi-automated method to perform best estimate of transformer parameters. The aim of the project is to use two-port network model to estimate the parameters for any transformer model using transmission parameters with less variable. The obtained data are analysed and compared with the corresponding values in different methods. It starts from an ideal and simplified transformer models, which applies one-port network on the transformer to be tested. The method of least squares is applied to obtain the best estimate input variables The optimization techniques, Lagrange Multiplier is also applied to minimise any discrepancy between the observed behaviour of a transformer and the predicted behaviour of the model. Analysis of non-linearity effects on transformer is the rest part of the project which involves identifying the characteristics in terms of magnetic field and current.
Motivation
The demand for electrical power is significantly increasing in our world. This shows that the number of power transformers is growing enormously, which play main role by stepping up and down voltage levels within transmission network and also used in electronic equipment. Thus, while maintaining existing transformers and designing new transformer, especially for low voltage transformers, accuracy of transformer parameters should be given also one of the priorities. Our project, “Measurement of Transformer Parameter” has significance in this aspect as it investigates the methods used for estimating transformer parameter, which is capable of providing more accurate values of the parameters.
Objective
To develop a method for estimating the transformer parameters, the same transformers as the past project are used. To estimate the parameters, namely: winding resistance (R1, R2), winding leakage reactance (X1, X2), core resistance(Rc), and magnetizing reactance (Xm), four short circuit and open circuit tests are conducted on the transformer, setting it under unsaturated condition (linear model). From the test, the input and output voltages and currents of the transformer are measured. The 7th parameter is calculated through conducting a separate experiment, which involves winding a sensing coil on the transformer core.
Introduction
Transformer Parameter
Practically transformers produce loss during their operation life time. These losses are because of the electrical and mechanical characteristics of the transformers components, and thus they are considered as parameters to model a transformer as an equivalent circuit[1]. The seven parameters of transformers are the following: -R1, R2: Represents the power loss due to the resistive characteristics of the windings -X1, X2: Represents the inductive property of the windings winding leakage reactance -Rc: Represents the eddy current and hysteresis power loss of the core -Xm: Represents the magnetization power needed to drive flux through the core -n(or a): the ration of number of turns of primary to secondary winding
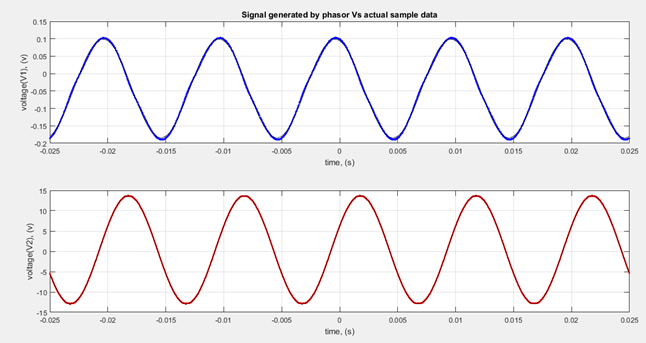
Method of Least Square for Phasors
Applying the fourier series theory [3] for a periodic function , having frequency of ω and N sample data, it can be represented as an infinite sum of cosine and sine terms of descrete frequency of integer multiple of ω.
Previous Study
The previous project, “Estimation and Measurement of Transformer Parameters” has been taken as the basic input for our project. Developing Matlab code for least Square Spectral Analysis performed on the measured voltage and current values, applying T-parameters used to estimate the seven transformer parameters under linear condition, and developing non-linear model of transformer are the other aims of the project.
Reference
[1]Soong, WL and Allison, AG 2014, ‘Electric Energy Systems’, School of Electrical and Electronic Engineering, University of Adelaide, SA. [2]P.C. Sen, "Principle of Electric Machine and Power Electronics", 2th ed. Ontario, Canada, Ch. 2 sec 2.2, pp. 50-53.