Projects:2017s1-181 BMW Autonomous Vehicle Project Camera Based Lane Detection in a Road Vehicle for Autonomous Driving

Introduction

Background

An automated vehicle [[1]] can be seen as a cognitive system and must handle all tasks compared to the human driver. The development of autonomous driving technology did not last long, but it develops very quickly, and far-reaching significance. Typically, 'Camera Based Lane Detection' method is an application of computer vision technique [[2]] in the autonomous driving field. It would develop the camera function application on a road vehicle instead of traditional human driver vision, such as lane detection or object tracking.

Motivation

Camera related to lane detection is the milestone of industrialization development. This project would provide an opportunity to understand the concepts of computer vision and realize how to use optical sensor, which is helpful for growth of Engineer's skills. Meanwhile, The project has a high commercial value and potential. Autonomous vehicle and computer vision techniques are developing rapidly, they would play an essential role in civilian and military area of human life in the future.

Projects Aims

The aim of this project is to determine the vehicle position on the road according to the lane on the street. To realise this aim, the priority work for project group is implementation of camera on a BMW vehicle, this camera needs to detect both cones and lands on the road. By using video processing technique, the expected outcome of this project is detecting the boundary lines of lanes and eliminating other elements. This project is focusing on straight lanes and curve detection algorithm, then integrate and apply this algorithm to a BMW vehicle. The algorithm should be effective in the conditions with flat road and regular illumination. For more complex environment such as, road with gradient or poor illuminations will be discussed in future research.

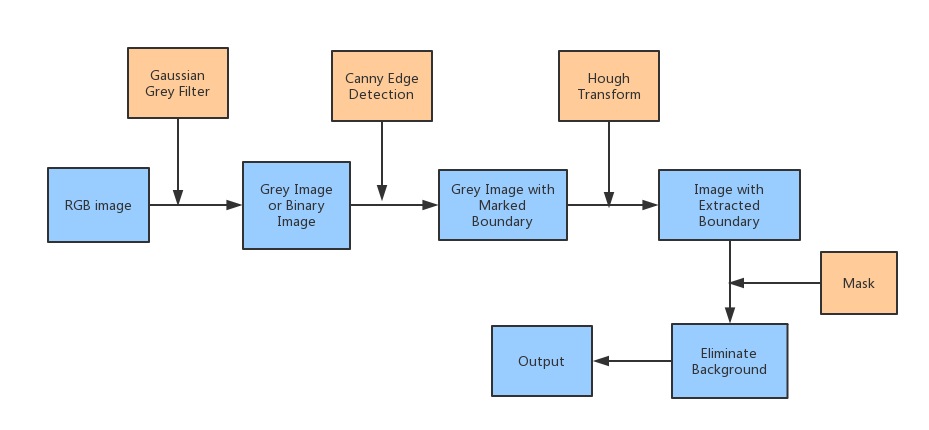
Lane Detection Theory

Gaussian Grey Filter

First step, we need an input RGB (red, green and blue) image, then apply Gaussian Grey filter on it, then we get our grey image. Gaussian blur also called Gaussian smoothing is a commonly used technique in image processing [2]. The equations [2] below are the Gaussian function in two dimensions.

G(x)=1/√(2πσ^2 ) e^(-(x^2+y^2)/(2σ^2 )) (1)

σ_r≈σ_X/(σ_f 2√π) (2)

Where the x is the distance from the origin in horizontal axis, y is the distance from the original in vertical axis. The coordinate x, y is controlled by the variance〖 σ〗^2, σ is the standard deviation of Gaussian distribution. Typically Gaussian filter is used to reduce image noise and detail. Colored image is complex and contains many details. Using grey image is easy for edge detection. According to Mark and Alberto [2], we know that Gaussian function removes the influence of points greater than 3σ in distance from the center of the template. Normally we set the σ value to one. If we need to remove more detail and noise we may need larger value of σ.

Canny Edge Detection

Canny edge detection results are easily affected by image noise, so it is important to filter out the noise before doing edge detection. As we mentioned above, the Gaussian function will be used when the image blurring filter is used. This function works like a low-pass filter; it attenuates high frequency signals, and passes the low frequency signal [2]. Then the Gaussian filter is applied to convolve with the grey image. This step will smoothing the image and reduces noise during edge detector [3].

G=√(G_x^2+G_y^2 ) (3) θ=atan2(G_y,G_x ) (4)

Next step is finding the intensity gradient of the image. The edge in the image may point in many different directions [3], so Canny edge detection algorithm use filter to detect horizontal, vertical and diagonal edges in the grey image. As we can see the equations above, G_x and G_y are first derivative in horizontal direction and vertical direction respectively [3]. Where the value of G can be found by using formula 4. Next step is to applying non-maximum suppression. This is an edge thinning technique [3]. After applying gradient calculation, the edges we extracted are still ambiguous. The reason is the gradient we found is the color difference between every two pixel, but difference we found may not be the largest value in a certain zone.

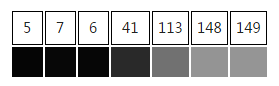
As we can see from the figure above, this is a one-dimensional signal. If we need to find the edge in the signal we may say that there should be an edge between 4th and 5th pixels. However, the intensity difference between them are not the largest one, the intensity of the 7th pixel is larger than the 5th intensity, therefore we need to set a threshold value to justify how large the intensity difference between adjacent pixels must be for us to confirm the edge [4]. That is the reason we need to apply double threshold. We need to set two threshold values. If the intensity difference is greater than the higher threshold, it will be marked as a strong edge pixel; if the intensity difference is smaller than the higher threshold but greater than the lower threshold, it will be marked as a weak edge pixel; otherwise this edge will be suppressed [3]. The last step of confirming edges is track edges by hysteresis. After filtering by double threshold, we can confirm the strong edge pixels should be included in the final edge image. The problem is how to confirm these weak edge pixels. According to blob extraction [5], for weak edge pixel, detect if there any strong edge pixel involved within 8-connected neighborhood pixel. Once there is an strong edge detected we can say this weak edge is included.

Hough Transform

The core idea of Hough transformation is to build coordinate system to represent any straight line, curve or circle on the image, then convert the straight line, curve or circle to parameter space. As this project is about lane detection, so only straight line and curve need to be fitted. Normally, the rectangular coordinate and polar parameter space will be applied to support Hough transformation making lane detection, the straight line or curve in rectangular coordinate is still a straight line or curve but in the parameter space is one point. One pixel in rectangular coordinate is one (x, y) point but in the parameter space is one straight line or sine curve. In other words, the parameter space can control the curve and straight line on the real image. So, adjusting the parameters relates to the function in MATLAB or OpenCV can draw the straight line or curve on the image. For example: The function of straight line in polar coordinate is r = x cosϴ + y sinϴ, Polar parameter space will be applied to express straight line. The character “r” is the radius between the origin points with closest point on the straight line, “ϴ” is the intersection angle between x-axis and the line which make connection from the closest point to origin point. The graph below shows the image get Hough transformation with MATLAB codes (in appendix D Hough Transformation)

Inverse Perspective Mapping

In this project, there are four coordinate system designs, which are the world coordinate system, camera coordinate system, image coordinate system and pixel coordinate system. The world coordinate system can also be called a vehicle coordinate system whose function is to define the position of the vehicle in the actual world. The camera coordinate system is based on the position where the camera is installed on the vehicle. The function is to determine the captured image parameters by measuring the height and angle of the camera's installation. The image coordinate system is used to measure the coordinates of the picture taken by the camera, which is the position of the pixel in the image in physical units (for example, millimetres). The pixel coordinate system is the image coordinate system in pixels. The storage form of the image is an array of M × N, and the value of each element in the image of the M rows and N columns represents the gradation of the image points. Inverse perspective mapping (IPM) is usually used to correct distorted images. In the study of autonomous vehicle vision system, since the pitch angle between the camera and the ground is not zero, the camera acquires the picture that's not the orthogonal projection of the road. The road image obtained by the vehicle camera has a substantial camera perspective effect. It is mainly shown that the lane lines at the bottom of the acquired image are straight, but the lane lines near the vanishing point become the compound curves. Apparently, the parallel-plane structure in the image coordinates system is more complicated than actual road model in the world coordinate system, especially curvature detection. The purpose of inverse perspective mapping is to correct the image in the form of an orthogonal projection, which is also to prepare the detection for road curvature. In the first part of this section, the construction of the pixel coordinate system and the world coordinate system was mentioned, and the result of the inverse perspective transformation is the conversion between the two coordinate systems

Least Squares

The least squares is a kind of mathematical optimisation technique. It matches the best function by minimising the square of the error. The polynomial of the least squares method is used to perform the curve fitting. The principle is to fit an approximate curve based on the coordinates of the scanned point in the image, which curve does not need to pass exactly these scanned points. In the image processing, each scanning point is a pixel; a fitting curve can be obtained by these pixels. A curve could be fitted by ‘polyfit’ function in the MATLAB.

Team

Team Member

Lai Wei

Lei Zhou

Sheng Gao

Zheng Xu

Supervisor

Prof. Nesimi Ertugrul

Robert Dollinger

Dr. Brain Ng