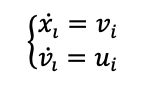Projects:2019s2-23301 Robust Formation Control for Multi-Vehicle Systems

Formation control has been widely used in the control of robots, sicne it can improve the overall efficency of the system. In this project, we aim to design a robust formation control for multi-vehicle system, in which the system can deal with at least one network problem or physical failure.

Introduction

Formation control of multi-agent systems (MASs) has been widely used for cooperative tasks in such applications as terrain exploration, mobile networks and traffic control. However, the communication-induced problems and the high failure risk of increasing equipments has created a number of challenges for the security of MASs. The objective of this project is to design a robust formation control strategy for a multi-vehicle system against communication and physical failures (e.g., network attacks, link failures, packet dropouts, sensor/actuator faults).

The vehicles are designed to detect the local environments by visual navigation and achieve a self-organisation formation. The robust fault-tolerant control strategy is investigated to deal with at leas one network problem or physical failure. The effectiveness of the formation control strategy and its robustness should be verified by both simulations and experiments. Potential applications are in large flexibility MASs and high-security Cyber-Physical Systems. Currently, our lab is equipped with a multi-vehicle platform, consisting of quadrotors, ground robots and camera location systems. Algorithms are developed by either Matlab Code or C language. MATLAB, Simulink, OpenGL, Motive and Visual Studio are possible softwares to be chosen for this project.

Project team

Student members

• Abdul Rahim Mohammad
• Jie Yang
• Kamalpreet Singh
• Zirui Xie

Supervisors

• Prof. Peng Shi
• Prof. Cheng-Chew Lim

Advisors

• Xin Yuan
• Yuan Sun
• Yang Fei
• Zhi Lian

Objectives

Design a robust formation control approach for multi-vehicle system to achieve:

• Self-decision making
• Environment detection
• Communication
• Obstacle avoidance
• Tolerance to physical or network problem

Background

Autonomous Control System

Autonomous control system has the power and ability for self-governance in the performance of control functions. They’re composed of a collection of hardware and software, which can perform the necessary control functions without intervention, or over extended time periods. There’re several degrees of autonomy. Conventional fixed controllers can be considered to have a restricted class of plant parameter variations and disturbances, while in a high degree of autonomy, controller must be able to perform a number of functions beyond conventional functions, such as regulation or tracking.

Agent

For the most part, we are happy to accept computers as obedient, literal, unimaginative servants. For many applications, it is entirely acceptable. However, for an increasingly large number of applications, we require systems that can decide for themselves what they need to do in order to achieve the objectives that we delegate to them. Such computer systems are known as agents. Agents that must operate robustly in rapidly changing, unpredictable, or open environments, where there is a significant possibility that actions can fail, are known as intelligent agents, or sometimes autonomous agents.

Multi Agent System

A group of loosely connected autonomous agents act in an environment to achieve a common goal. This is done by cooperating, and sharing knowledge with each other Multi-agent systems have been widely adopted in many application domains because of the beneficial advantages offered. Some of the benefits available by using MAS technology in large systems are

• An increase in the speed and efficiency of the operation due to parallel computation and asynchronous operation
• A graceful degradation of the system when one or more of the agents fail. It thereby increases the reliability and robustness of the system
• Scalability and flexibility- Agents can be added as and when necessary
• Reduced cost- This is because individual agents cost much less than a centralized architecture
• Reusability-Agents have a modular structure and they can be easily replaced in other systems or be upgraded more easily than a monolithic system

Formation Control

Formation of a multi-agent system is a composed of a group of specific agents, communication among agents, and geometrical information of agents. This project focuses on the formation control of the multi-vehicle system. The aim of formation control is to design a controller that has the ability to bring the agents to a desired geometric shape by assigning local control laws to individual agents.

Methodology

Detection

1. Detect objects in immediate surroundings using LiDAR for distance measurement and monovision sensor for object classification
3. Use angular rotation from IMUs and distance to object as polar coordinates for localisation
5. Calculate global coordinate points of objects based on polar coordinates
7. Pass object data to Agent unit for formation control

The detection module is used to detect localised environmental information using its many sensors such as vision sensor, SONAR Ultrasonic sensor, LiDAR ToF (Time-of-Flight) sensor and IMU. The detection module achieves sensing through heterogeneous acquisition mechanism also referred to as multimodal sensing. Multimodal sensing is necessary because it allows us to capture environmental information more vividly than using single sensor based ranging. Data gathered from various sensors is fused together within the agent through the process called Data fusion which allows multimodal data streams to jointly analyze captured sensing data. LiDAR and SONAR sensors will provide ranging information for object detection during the hypothesis generation and the vision sensor will provide the system with object’s shape parameters for hypothesis verification phase. The detection module uses ultrasonic sensors for their wide cone of detection and LiDAR for its accuracy to sweep the immediate area, this allows the rovers to mark any obstacles within its path. This is in contrast to using multiple sensors for ranging which increases computational needs and power consumption on low energy hardware where the rovers will be ultimately planned to be deployed. Detection occurs in two phases, first of which is the hypothesis generation phase. Hypothesis generation phase is when the ranging sensors detect an obstacle within their detection zone and consider the hypotheses that the obstacle is a fellow agent. The rover will then focus its efforts towards identifying the obstacle through the use of vision sensor. The second phase, hypothesis verification phase will use the vision sensor to verify our hypotheses. The vision sensor will extract frames through the real time feed and passes these frames to our YOLOv3 model that has been pretrained with a classifier. The classifier is trained using 800 images manually labelled to train the classifier. The model was trained for 900992 images with an average loss ratio of 0.016559. To ensure robustness within the system and to optimize the detection rate and computational needs, the vision sensor only captures frames every 100 milliseconds and process these frames through the object detection model.

Fig 1

The distance data is filtered through Alpha trimmed mean filter and a Kalman filter before being packed from the main function to support functions indicated with “Filtered Distance Data” in the Fig 2. Orientation data is filtered through complementary filter and sent from the main function to support functions for the hypothesis generation phase. Hypothesis is verified in the Hypothesis verification phase when data from the vision sensor returns a state value which is “0” for no rover detection and “1” for any rover detected. The data is then fused together and passed to the support function that calculates rectangular coordinates using the polar coordinates from distance for radius and angle from IMU sensor. The rover is now localized within its frame and this value is passed over to support functions. Support functions calculate the global frame using the rover’s coordinates as a reference point. Adding the local coordinates to the self-reference point allows us to locate rovers in the global frame.

Fig 2

The following filters are necessary for robust performance of the detection module, they also provide a level of fault tolerance to the system.

Kalman Filter

Kalman filter is a recursive algorithm that provides the optimal estimate of the system state, given the noise in the system. It tries to achieve the optimal estimation of the unknown configuration based on the previous estimate and new measurement data. The filter updates at fixed time intervals specified in the model. Kalman filter is used as a fault tolerant system that will estimate the optimum distance to the object even if the LiDAR and SONAR ranging sensors provide faulty ranging data. The filter will approach the optimal estimate with increase in iterations of the filter.

Complementary Filter

Complementary filter is a recursive algorithm that provides the optimal estimate of the gyration data. It tries to achieve the optimal estimation of the angular position and gyration based on the previous estimate and a combination of low pass and high pass filters. Complementary filter is used to take slow moving signals from accelerometer and fast-moving signals from a gyroscope and combine them as sensor fusion. Data from accelerometer and gyroscope are enough to estimate angular positions as such there are the only inputs to the Complementary filter. Data from the gyroscope is used because it is very precise and not susceptible to external forces. Data from the accelerometer is used as it is less susceptible to noise due to drift. The filter updates these measurements at fixed time intervals specified in the model considering previous measurements while estimating new data.

Alpha Trimmed Mean Filter

Alpha trimmed mean filters are a variation of adaptive mean filters that are especially effective against additive gaussian noise. The filter is an adaptation from image processing used to remove impulse noise as they are a good compromise between moving mean filter and median filter. They are used if the nature of noise in the system deviates from the gaussian with impulsive noise components. The filter is a moving window-based filter which iterates over the continuous stream of data from ranging sensors over a given window size of w and trimming factor of α. Adaptive alpha trimmed filters allow for the flexibility of choosing α based on the local noise statistics.

Obstacle Avoidance

Artificial Potential Field method (APF)

The Artificial Potential Field method (APF), which was generated by Khatib in 1986, is introduced in this project to help robots to avoid obstacles. As shown in the Fig 4, the robot’s moving area is simplified into 2D-plan (a virtual potential field). In addition, the robot, obstacles and the desired location are all simplified into points. In this area, obstacles provide the repulsion to the robots, and the repulsion must become bigger when the robots are closer to the obstacles. It should be noted that there is a detection range of the obstacle. In other words, if the robots are in this range , then the robots must be affected by the repulsion from the obstacles. Otherwise, the repulsion is zero. The desired location provides the traction to the robot, and the traction must become smaller when the robots are closer to the desired location. Eventually, the robots must move under the resultant of the repulsion and the traction.

Fig 3

Issues with APF & Improved APF

The APF has some issues, including the unreachable target issue and the local minima issue. The unreachable target means the robot cannot achieve the desired location, and the robot can be in a state of shock, like the Fig 4 shown. To be detailed, the unreachable target issue happens when the obstacles are close to the desired location. At the same time, the robot and the desired location are both in the detection range of the obstacle. In this case, the desired location is located between the robot and the obstacle. In addition, as mentioned above, the repulsion from the obstacle must become bigger when the robot is closer to the obstacle. However, the traction must become smaller when the robot is closer to the desired location. As a result, the robot must be pushed back by the repulsive force when the robot becomes closer to the desired location and the obstacle. After this, the traction must become bigger and the repulsion must become smaller, since the distance between the robot and the desired location (and the obstacle) becomes bigger now. As a result, the robot must be pulled forward by the traction. Eventually, the robot must repeat the process of “back and forward” (in a state of shock). For the issue of the local minima, the resultant of the repulsion and the traction is zero in some points, which are not the desired location, so that the robot stops moving and cannot arrive the desired location.

Fig 4

Fig 5

For the unreachable target issue, the relative distance between the robot and the desired location must be introduced into the repulsive field function. Therefore, the procedures of this method just need to update the equation of the repulsive field function, and other procedures are all the same as the traditional one. In terms of the local minima issue, the “Virtual Obstacle” method is introduced. The difference between traditonal APF approach vs the improved APF are shown in the Fig 5

The procedures of the strategy to escape the local minimum point are:

• Identify if the robot is in the local minimum point every 2 steps.
• If the robot is trapped in the local minimum point, then the strategy of escaping the local minimum point must be activated.
• The strategy here is that the robot must treat the current local minimum point as a “virtual obstacle”. Then, the system re-calculates the forces around the robot. Finally, the system finds out the direction of the resultant force.
• The robot moves toward this direction with a small step

Formation Control

Time-varying Formation Control

The major task of formation control is to calculate desired positions by individual agents themselves. It takes positions and velocities information from the detection module and output a controlled output which in our implementation is velocities and accelerations. The control input is the formation position we delegated for the system and the state vector is the positions and velocities information of each nodes. These two variables form the node dynamics of the system. A consensus protocol has been designed to control these variables for each agent.

In our system, the main focus is the design of achieving desired position with desired velocity. Therefore, on the formation control level the system can be literally simplified as a second order linear system. A double integrator can approximately describe the dynamics of each as:

where x and v refer to the positions and velocities of each agent respectively and u is the control input of the 𝑖th agent.As the motion of agents along each axis is independent, this control law can also be adapted to higher dimensional cases with using Kronecker product.

Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Theta_i(t)=[x_i(t),v_i(t)]^T } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle B_1=[1,0]^T } , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle B_2=[0,1]^T } . The time-varying system for agent dynamics can then be reformatted as:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \dot{\Theta_1}(t)=B_1 B^T_2 \Theta_i(t)+B_2 u_i(t) }

Define Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_(t)=[h_(ix)(t),h_(iv)(t)],i=1,2,...,N } as the desired position and velocity of agent Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i } where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i(t) } is a continuously differentiable vector. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h(t)=[h^T_1(t),h^T_2(t),...,h^T_N(t)]^T } is a column vector that contains desired formation for all the agents. A graphical explanation of these variables has been shown in the figure below

A time-varying formation can then be descripted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i </mat> for an MVS. For the system to achieve the desired formation function, there will be a controller that perform the <math> \Theta_i } under certain initial condition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Theta_(i0) } and input Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i } such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lim_{t \to \infty} (\Theta_i(t)-h_i(t))=0 } .

Motion Control

Fig 8

Fig 9

The formation control and obstacle avoidance algorithms were formed in MATLAB which would provide the continuous stream of final points. An algorithm to send these data points from MATLAB to CoppeliaSim was deigned by the motion control module. These final points were then fed into the embedded Lua script and the coordinates were sent to CoppeliaSim by the help of remote API method.

As seen in Fig 8, MATLAB is used to form a connection with the CoppeliaSim scene through a function MoveSpin which contains necessary commands that help in establishing a connection and asking the user for the final points to be transferred to CoppeliaSim.

This packed data from the MATLAB was transferred into a child script attached to a object which acted as a connection maker in the system. data points are sent to the respective robot, the next process is the planning path of the motion. In a robotic Lua script, the desired points are read and fed into the control. the initial and the final points interact points to find d and θ shown in Fig 9. These velocities (v_x (t),v_y (t) and ω(t)) are the global velocities that help in planning the path but they need to be changed into the reference frame velocities((v (t), v_n (t), ω(t))) also seen in Fig 9

• x,y,θ- Robots position (x,y) and the angle that is relative to the front
• d[m]- the distance between the wheels and centre
• v_0,v_1,v_2(m/s)- wheel linear velocities
• ω_0,ω_1,ω_2 (rad/s)- wheels angular velocities
• f_0,f_1,f_2 (N)- wheel traction force
• T_0,T_1,T_2 [N.m] – torque on the wheels
• v,vn [m/s]- Robot linear velocity
• ω[rad/s]-Robot Angular velocity
• F_v,F_vn [N]-Robot traction force along v,vn

T[N.m]-Robot torque(respect to ω)

Results

Detection Results

Local and Global Coordinates

The system is capable of calculating local and global coordinates based on the ranging data provided by LiDAR sensor. Local coordinates are based on the local frame where the center of the rover on which the sensors are mounted, this is referred to as self-reference. The local frame assumes the center of the coordinate plane (0,0) as the center of the rover and the distance of the object detected as input to support functions. The support functions transform the polar coordinates to rectangular coordinates LiDAR’s distance(r) and IMU rotation(θ). Global coordinates are calculated by using the position of the current rover in simulation space accessed through the CoppeliaSim’s Remote API functions. The local frame is then concatenated to the rover position in the rectangular coordinates. Fig 1 shows the local coordinates and global coordinates displayed in the output of object detection.

Fig 1

Actual Distance (m)	LiDAR Distance	Kalman Filtered(1st iter)	Kalman Filtered (3rd iter)
1.650	1.649	1.669	1.651
1.154	1.154	1.171	1.158
1.018	1.017	1.030	1.022
1.652	1.649	1.670	1.653

Fig 2

Although the LiDAR sensor is accurate in ranging operations, it becomes necessary to filter out noise within the system introduced over time either due to the rover’s own movement or environmental conditions. Kalman filter is used as a fault tolerant system that will estimate the optimum distance to the object even if the LiDAR and SONAR ranging sensors fail or provide faulty estimates. Kalman filter works by estimating Kalman gain which is derived from the incoming sensor data like LiDAR ranging data, and prediction-based estimates from the mathematical model of the system designed beforehand. Every iteration of the Kalman filter increases the accuracy of the estimates giving robust ranging data even under unsuitable environmental conditions or faulty sensor data. Kalman filter, however, does not account for the complete sensor failure as it relies on incoming data to estimate the distance. Fault tolerance in that case is achieved by using the alternate ranging sensor such as SONAR or in cases when both sensors fail, active triangulation can be fed as an input to the filter. The Kalman estimates are consistently 3-10 mm higher than the actual distance, this is due to imperfect modelling of the system in the filter, some calibration of the model is required before the filter can be used for maximum accuracy.

Actual X(in meters)	Actual Y	Localised X	Localised Y
1.90	1.05	1.40	1.10
1.34	1.03	1.66	1.07
1.07	2.10	1.069	1.99
3.99	2.01	3.76	2.13

Fig 3

As can be seen from Fig 3 and the table, there is some discrepancy in the accuracy of the localized coordinate frames. This is due to the constant rotation of the rover that changes the IMU’s rotation data that in turn affects the polar to rectangular coordinate transformation. This error can be mitigated to by using only the first measured distance (first detection values) as the only measurement to consider as the accurate measurement. The error in the distance is an average of 0.265m i.e. 26mm. This error is due to the nature of detection at the point of contact of LiDAR instead of the center of the rover as the actual coordinates denote. This error can be compensated by adding the half width of the rover as calibration data to the distance measured.

Obstacle Avoidance Results

The program starts from setting the coordinates for the initial positions, the desired location, the obstacles’ positions and the parameters of obstacle avoidance algorithm. Then, the system must judge if the robot arrives the desired location. If the robot arrives the desired location, the program can be end. Otherwise, the program must compute the traction force (vector). The program must judge if the robot is affected by the obstacles around it before computing the repulsion force (vector). After that, the program must add traction vector and repulsion vector so that the resultant force vector can be obtained. It should be noted that the resultant vector can be used to find out the direction of the resultant force. Then, the robot must move toward this direction that is provided by last step with a step size, which is must be small enough so that no collision is possible when robot moves to next position. In addition, the size of the robot and the obstacles are set. A method of setting size of obstacles and robots is introduced in . In this method, the size of robot is suggested to be added to the size of the obstacle. In conclusion, in this method, the robot is still a point and the size of obstacle is combined with the size of robot and the size of the original obstacle. The improved APF simulation results show that both local minima issue and unreachable target issue can be overcome. The simulation results for the local minima issue are shown in Fig 4 and simulation results for the unreachable target issue are shown in Fig 5.

Fig 4

Fig 5

Motion Control Results

Fig 6

The Motion control algorithm created the following trajectories(Fig 6). The blue trajectory is formed by the two-wheel differential drive and the green trajectory is formed by the 3-wheel Omni wheel drive.

The test was run for 3 times in both the cases and the graphs clearly show that the trajectory formed by the Omni wheel drive is more in shape than the counterpart. It is important to identify the far corners of the trajectories, the corners for the 3-wheel drive are more pointed than the 2-wheel drive. The above observation took place because the differential drive had a front face because of which it could not align itself towards the desired position. Since any robot path planning is the smallest path due to non-alignment with the desired point it could not move in the backward direction because of which the circular curves were formed at the ends of the graph that moved the robot to first align itself and then follow the trajectory. On the contrary, in a 3-wheel drive, there was no front face and the robot could align to the desired point and moved along the trajectories. The mean deviation in the 2-wheel drive case was 28% more than the 3-wheel drive case (compared along the y-axis of the movement). Hence three-wheel robots were selected over the 2-wheel differential drive.

PID

PID controllers are an important part in the motion control. Since the motion also brings the concept of momentum, a robot while moving in any direction tends to stay in motion even if the desired point is achieved. This phenomenon brings an overshoot in the system.

Fig 7

• CASE I-The velocity constant was kept at 40 m/s and the value of Kp and Kd was 0.6 and 2 respectively.
• CASE II- The velocity constant was kept at 45 m/s and the value of Kp and Kd was 0.7 and 1.75 respectively.
  
• CASE III- The velocity constant was kept at 60 m/s and the value of Kp and Kd was 0.6 and 3 respectively.

Case II indicated as yellow lines in both the graphs showed a medium quality profile with the period of 5.78 seconds, peak overshoot of 0.0156m, the constant error of 0.0028 meters and average speed of 0.85 m/s. This was the recommended constant values that were to be used in the system.

One of the aims of the project was to develop a robust system. The robustness in the motion module can be analysed by keeping the velocity of one wheel to be zero or in other terms if one wheel in the 3-wheel system does not work. The normal system with two wheels might not work due to the dependence of the system on the motion of 2 wheels but the 3 wheel system is geometrically structured such that the rollers in the third wheel act as a third wheel in the system with the driving force from the other two wheels. The healty system is represented as dashed line, when all the 3 wheels in the system are working and the blue line shows the faulty system that indicates only 2 wheels are operational(Fig 7).

Reference

[1] Wooldridge, M (2002). An Introduction to MultiAgent Systems. John Wiley & Sons. ISBN 978-0-471-49691-5

[2] Balaji, P., & Srinivasan, D. (2010). An introduction to multi-agent systems. Studies in Computational Intelligence, 310, 1-27.

[3] Hong-Jun M., & Guang-Hong Y. (2016). Adaptive Fault Tolerant Control of Cooperative Heterogeneous Systems With Actuator Faults and Unreliable Interconnections. IEEE Transactions on Automatic Control, 61(11), 3240-3255.

[4] Oh k, Park M, & Ahn H. (2015). A survey of multi-agent formation control. Automatica, 53, 424-440.

[5] Khatib, O. (1986). Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. The International Journal of Robotics Research, 5(1), 90–98. https://doi.org/10.1177/027836498600500106