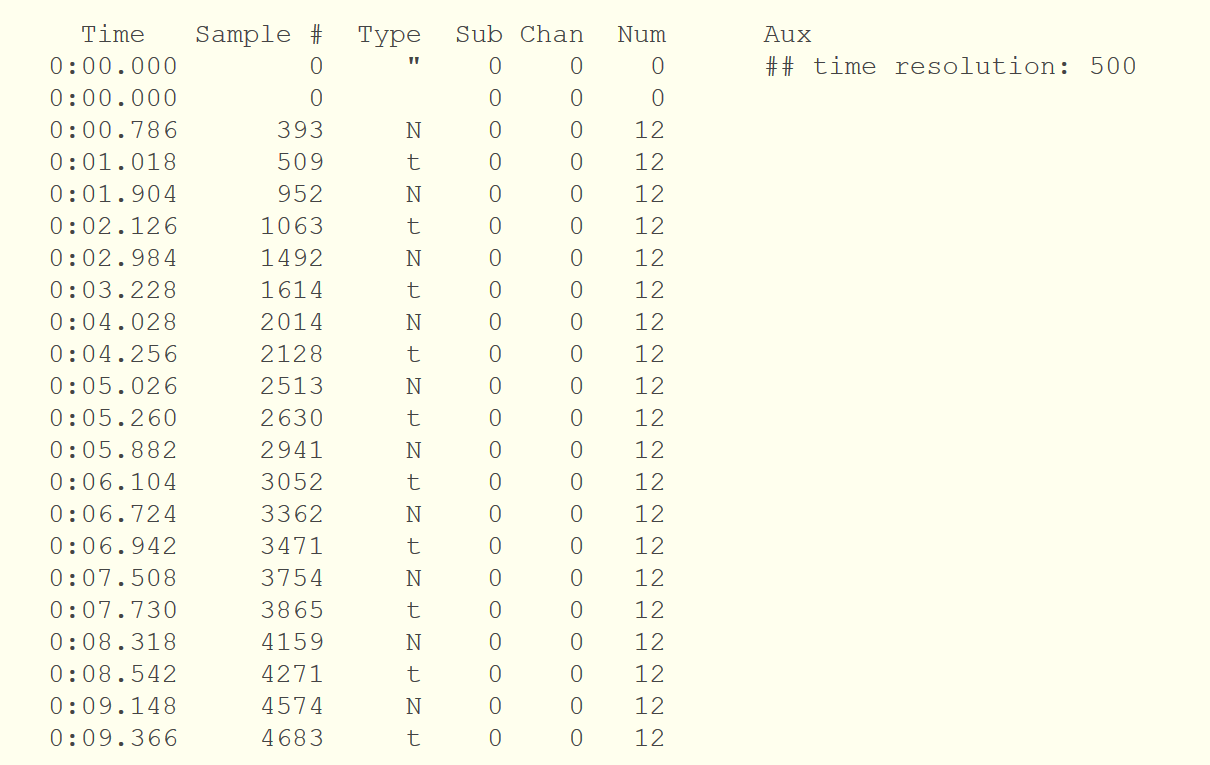
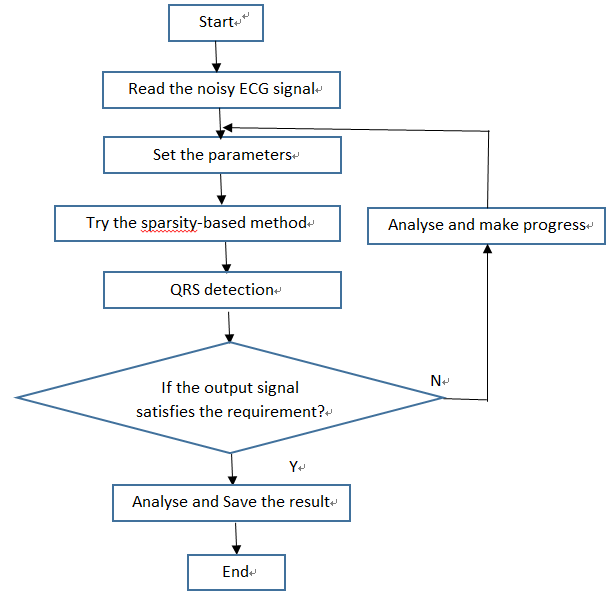
Projects:2016s1-131 ECG Enhancement with Advanced Signal Processing

Topic

ECG Enhancement with Advanced Signal Processing

Supervisors

Dr. Brian Ng

Prof. Mathias Baumert

Team Members

Yang Lin

Yingtong Guo

Introduction

The electrocardiogram (ECG) recording plays an important role in medical applications. However, it is easily affected by sources [2]. In this project, we are intend to enhance ECG signals by using recent advances in digital signal processing which is based on the sparsity –based signal processing. Three ECG databases and one optional database are used to implement the approach. Generally, the desired ECG recordings are gained from websites and then according to different ECG signals, the sparsity-based method is used with different parameters. After that, the performance of the method is evaluated by comparing the accuracy of the RR interval measurements, obtained from the Pan Tompkins QRS detection algorithm.

Motivation

The ECG signals are measured from the body surface so it is easy to be contaminated by body and instruments. It is essential for doctors to diagnose the diseases accurately by analysis of ECG signals and actually, all the waves of ECG signals have a certain pattern which have a predictable time duration, a range of acceptable amplitudes and a typical morphology which means that any deviation from the normal pattern is potentially not healthy [1]. Therefore, the noise or artefacts in the ECG signals can influence the doctors’ diagnosis and that noise in the ECG ideally should be removed before doctors’ diagnosis. That is the reason why we need ECG signal processing. In this project, the noise in the ECG signals will be removed or reduced and ECG will be enhanced with digital signal processing techniques so the doctor can analyze the real signal which should make the diagnosis more accurate, stable and reliable.

Previous Studies

This project is not a follow-up project but it is based on the work of Ning and Selesnick [2]. In their paper, some detailed denosing problem and proposed algorithm has been discussed. The most important thing is that the sparsity-based method has been introduced which make it possible to implement in ECG signals [2]. In addition to that, the QRS detection algorithm is named Pan Tompkins [3] which is reliable to detect the QRS complexes. It has a good result for the standard 24h MIT/BIH arrhythmia database so it can be used to test our project’s result. In this project, three databases and one optional database are chosen from physionet website to verify the sparsity-based method in the work of Ning and Selesnick and use Pan Tompkins QRS detection algorithm to check the result.

Objectives

The aim of this project is to improve the ECG signals in three databases and one optional database. The objectives are: • Reduce the influence of noise which mainly focus on motion artefacts on ECG signal in the chosen database to provide better result for doctors. • Investigate sparsity-based separation methods for QRS detection and compare the result to previous research. • For the optional database, separate desired clean ECG signal from mixed ECG recording.

Background

ECG Basics

ECG is an approach that measures and records the electrical activity of the heart. It can be sensed by monitoring electrodes which are placed on the body surface. The basic information can be measured from the ECG signals is the heart rate and heart rhythm. For example, a normal person’s heart rate is from 60 to 100 beats per minute [1]. Therefore, the clinicians can diagnose the patients through the heart rate and rhythm. Actually, each electrical activity of heart has a distinctive waveform. Figure shows that a normal ECG signal consists of P wave, QRS complex and T wave [1]. The first one is called P wave which represents the depolarization of atria from the SA node to the AV node. Depolarization is the change in the cell’s membrane potential to a positive value. It is this change that generates the electrical impulse that starts the heart’s contraction so the P wave can be related with the contraction of the atria [1]. The QRS wave which looks like a small dip followed by a large spike and another dip represents the depolarization of the ventricles which can be also think as the contraction of the ventricles [1]. One thing noticed is that the P wave is smaller than the QRS complex. That is because the ventricles are the muscle pumps of the heart compared to the atria. After the QRS complex, there is the T wave which represents the repolarization of the ventricles [16]. Repolarization is the opposite of the depolarization which returns the membrane back to a negative state [1].

Noise and Artifacts

In signal processing, noise is an unwanted component that a signal may suffer during transmission, processing and conversion. Basically, there are mainly 4 kinds of noises which possibly interfere the ECG signals: • Power line interference is the most common noise. It comes from patients’ cables and can be easily found since the interfering voltage in the ECG signal will have frequency 60 Hz [18]. What is more, it can be regarded as sinusoids and combination of sinusoids [4]. Despite the fact that hardware system can remove part of the signal interference, the 60Hz of power line interference still exists [17]. • Muscle contractions (EMG) is caused by the contraction of other muscles besides the heart [2]. That contraction can also produce depolarization and repolarization which can influence the ECG signals. Moreover, it can be reasonably modelled as Gaussian distribution function. However, the variance is dependent on the environmental variables [4]. • Electrode contact noise is caused by the loss contact between the electrode and skin which can be permanent [4]. Figure 39 in Appendix shows it can cause sudden changes in amplitude of the signal. • Motion artefacts which due to vibrations or movement of the subject, resulting in a change to the skin voltage [4].

Sparsity-based method for removing noise

To remove the noise in ECG, actually there are many methods such as wavelet transform and adaptive filtering [7]. The wavelet transform is a time-scale transformation to optimize signal composition structure [6] and it will be described in detail in the next section. For Adaptive filtering method, a widely used one is the least mean squares (LMS) adaptive algorithm. As shown in figure 41 in Appendix, the basic idea of LMS filter is to keep a gradient based iterative solution [19]. The idea of noise reduction is to use the adaptive filter to estimate the effect of the secondary input on the primary signal (the filter output Yk) and subtract this from the primary signal [19]. For example, the problem of fetal heart beat measurement. The heartbeats of the fetal are often corrupted by the effect of mother’s heart [23]. In that case, the effect of the mother’s heart on the fetal will be estimated and subtract this from the primary signal, leaving an enhanced signal Ek which consists primarily of the fetal heartbeat signal.

BP and BPD

However, all those ways are not flexible enough and some important information may miss due to the noise is non-stationary and the overlap of signal and noise bandwidths. In Ning and Selesnick’s work, many algorithms based on sparsity-method for noise reduction have been introduced. If it is known that the signal which will be estimated has sparse Fourier coefficient, then sparsity-method can be used for denoising [5]. The basic idea about sparsity-method is to consider a system with the equation Y=Ax where A is an M x N matrix, y and x are length-M and length-N vectors respectively, where N>M. As the unknowns in the system are more than equations, the equation Y=Ax has infinitely many solutions. An l1-norm is used which is defined by:

                              （1）

An approach to solve Y=Ax is to minimize the sum of absolute value of x:

                            （2）

Where ||x||1 is the defined l1-norm. This problem is known as the basis pursuit (BP) problem which cannot be expressed in explicit form. One way to tackle the problem is to use an iterative numerical algorithm [5]. What is more, in real world y is usually noisy, the solution to the Y=Ax can be changed to minimize the cost function:

                (3)

This is the basis pursuit denoising (BPD) problem and similar to BP, the BPD problem can be solved by using an iterative numerical algorithm. In addition, note that ||x||1 is not differentiable since it is defined as the sum of absolute values [5]. The absolution value function is not differentiable at zero. That make the calculation difficult for large-scale problems. However, the BP and BPD problems are convex optimization so that some practical algorithms from optimization theory can be used such as iterative shrinkage (ISTA), fast ISTA (FISTA) and split variable augmented lagrangian shrinkage algorithm (SALSA) [5].