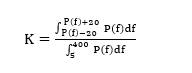Projects:2016s2-240 Electromyographic Signal Processing for Controlling an Exoskeleton

contents

Introduction

Background

The exoskeleton is a wearable device which can reduce physiotherapist intervention but ensure the efficacy of rehabilitation in the medical and health area, which can also help soldiers fight better because it can help them get better protection and carry more weapons and equipment in the military area. Recent years, researchers from around the world are working hard so that the exoskeleton can be widely used in practice.

EMG signal is a bio-medical signal which generated from muscle activities. EMG signal originates from motor neurons in the spinal cord, which is the part of the central nervous system. Motor neurons are in the cell body; their axons extend to the muscle fiber and couples fiber at the end plate area. Muscle movement is controlled by awareness, when the brain is excited and downward conduction, the somatosensory and dendrites of the motor neurons in the central nervous system generate electrical impulses under the stimulation from synapses. These electrical impulses are along the neurons of the axon conduction to the peripheral nerve and muscle contact. When the motor nerve contacts the muscle, the axon branches to many fibers, and each branch ends in the muscle fibers to form synapses, which are called motor end plate. The generated electrical impulses are broadcasting along muscle fibers, which cause a serious change inside muscle fibers, and then produce a contraction of muscle fibers. Therefore, a large number of muscle fibers produce muscle contraction. It can be seen that the spread of action potential of muscle fibers leads to the muscle contraction, while the spread of electrical signals in human soft tissue results in the current field, and the potential difference is represented between the detection electrodes, which is EMG signal [1]. Usually, the amplitude of EMG signal is between 50μV and 5mV. The bandwidth is of EMG signal is from 0—500Hz.

SEMG signal is a bioelectric signal released from the neuromuscular activity recorded by the electrode from the surface of the human skeletal muscle. Different muscle movement patterns are caused by different muscle contractions, and their accompanying SEMG signals are different. It can be used to research or detect the muscle bioelectric activity to determine muscle system skills as well as morphological changes and contribute to neuromuscular system research or provide diagnosis [2]. The frequency range of the SEMG signal is from 0 to 2000Hz, but from the perspective of intensity, SEMG signals are mainly distributed between 20 and 500Hz.

Aim

This project was based on signal processing and focused on developing algorithms for feature extraction and classification to control lower limbs of an exoskeleton. The feature extracted from the recorded EMG signal will be compared to the previous training recordings to identify what kind of movement the muscles are trying to implement.

The project built up a system that has following contents: 1) Surface EMG signals recording. 2) Surface EMG signal denoising. 3) Surface EMG feature extraction. 4) Feature comparing and recognizing with the help of previous data.

The outcome of the project is a control system that extracts the feature of the input EMG signal and then delivers the muscle state as an output to the motor control of the exoskeleton. The system is accurate and fast in real-time processing.

 
      System breakdown

Approach

In this project, three algorithms are used to analyze the EMG signal.

Process

Usually, different actions generate different powers, therefore, the muscle action ratio can be used. Muscle action ratio is measured by the contraction of muscle rigidity, and the degree of this contraction depends on the frequency of nervous fiber transfer impulse. Therefore, power ratio can be used to represent different EMG signal which generated from the variety of actions by the way of intensity estimation [3]. The value K can be used to represent this ratio. The steps of calculating this value K are the following: By frequency spectrum, find central frequency P(f); Calculating the power of a segment which is [P(f)-20, P(f)+20]; Dividing this calculated value by the whole segment value, the formula is

The reason for using the segment of 5Hz to 400Hz is the main frequency of SEMG signal is between 5Hz and 400Hz. Comparing this value K with reference signal recorded in the database, identify the threshold value. As shown in the following two charts, the shadow area is the power of the center frequency±20Hz; furthermore, many signals with smaller amplitudes existed when the muscle is contracted, so there is much more power speared out when the muscle is contracted. Therefore, the value K of the relaxed muscle is bigger that the value K of the contracted muscle. This is verified through the off-line test.

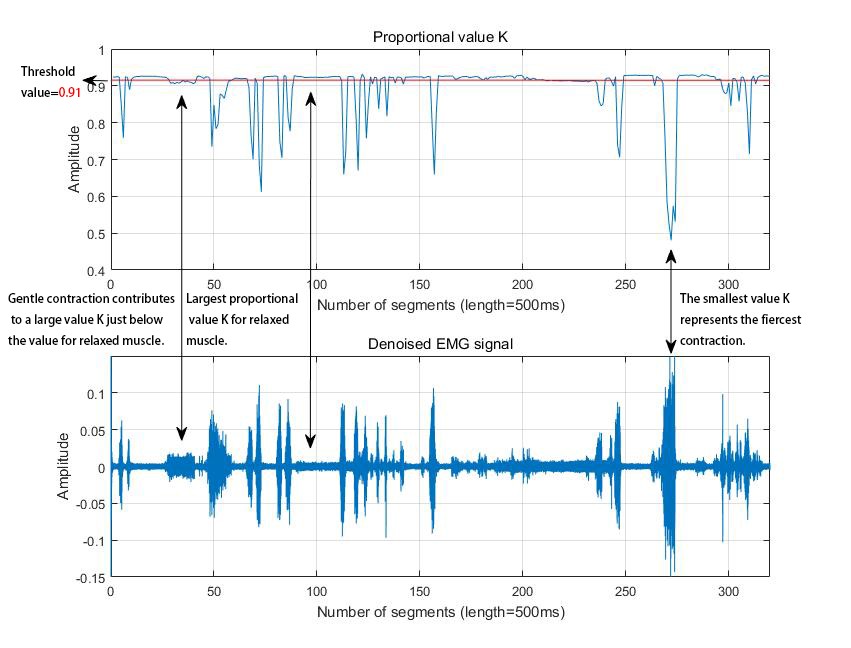
During the off-line analysis, as for the 64-channels SEMG signal motioned in the previous part, extracting one channel signal (assuming channel 1), the center frequency got is 76.29Hz. Figure 9 is the power spectrum of channel 1 signal, and its center frequency has been marked. Then using proportional value K to identify muscle action. Figure 10 is the plot of the calculated value K. Comparing with the corresponding time domain signal, it is suggested that the value K changes significantly when muscle switches from tight situation to relax situation and vice versa.

In real-time analysis, considering the condition of the muscle activity, the value K will be calculated every half second. Because the sampling frequency is 4000Hz, the data segment is 2000. Usually, the first step is to identify the threshold value K, which is operated through visual observation, because this value depends on who the subject is, which channel is used and the electrode placed on which muscle. The chart below is the value K captured in the real-time test, the threshold value is 0.91 this time. Then typing this value into the MATLAB code, the system will do the classification work automatically in the real-time experiment and the result will be displayed on the screen. If the calculated value K is bigger than the threshold value, then muscle is relaxed; if the calculated value K is smaller than the threshold value, then muscle is contracted.

                                       The value K with corresponding denoised EMG signal

Result

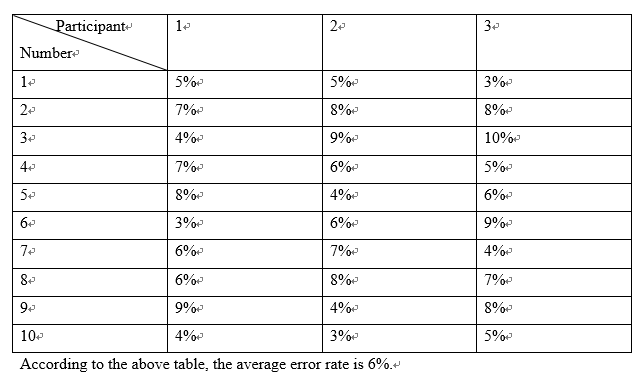
There were 3 female subjects participated in the real-time test, and their ages were 24, 25, 26 respectively. Each participant was tested 10 times for 50 seconds each time, which means 100 segments of data each time was processed. The following table illustrates the error rate for each time.

Autoregressive (AR) model coefficient estimation algorithm

Process

AR model coefficient estimation method is based on analyzing SEMG signals in the time domain. In detailed, as for the time sequence X_t, where t = 1, 2, 3, …, N, the AR_((n)) model of which can be represented as the linear fit of X_(t-1), X_(t-2), …, X_(t-n). It can be written as X_t=φ_1 X_(t-1) + φ_2 X_(t-2) + … + φ_n X_(t-n) + a_t, where a_t is the stationary white noise sequence with zero-mean and variance Var=σ_a^2. The coefficients of φ_1, φ_2 , …, φ_n and σ_a^2 are the parameters that need to be estimated. In this report, the least square method is used to estimate parameters, because it is simple, unbiased and high precision [29]. The matrix form of the signal can be expressed as the following equation. The order chosen for this AR model in this project is 15.

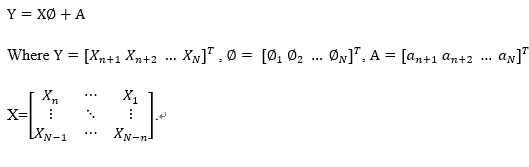
Result

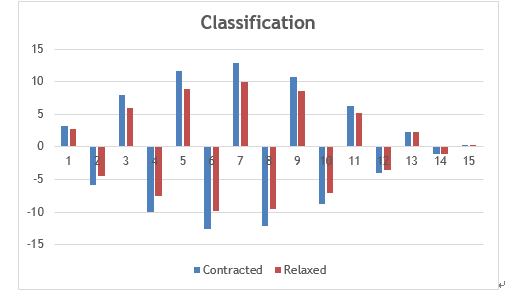
As mentioned above, the SEMG signal is still stored and processed every 0.5s. Because the sampling frequency is 4000Hz, each set of data contains 2000 sampling points. Then, building the AR model for each set of data through MATLAB, the coefficients matrix can be obtained. The following graph compares one set of the EMG signal in contracted pattern and one set of the EMG signal in the relaxed pattern.

According to the above tables and graph, what can be found is that as for the same pattern, the coefficients matrixes of the AR model are similar; as for different pattern, the coefficients matrixes of the AR model are significantly different. Utilizing different AR model matrixes to classify, the different pattern results can be obtained, and that can be done easily through the BP neural network. 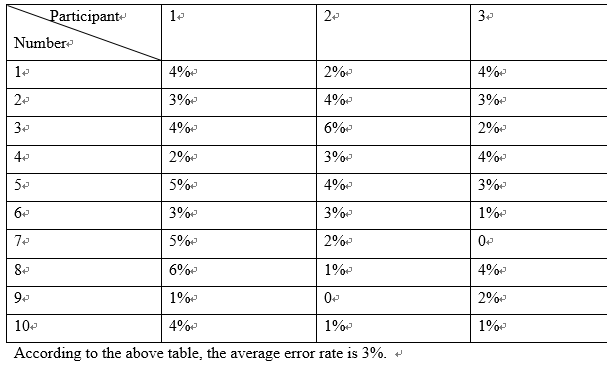During the real-time test, each participant was tested 10 times for 50 seconds each time, which means 100 segments of data each time was processed. Subjects are the same as mentioned above. The following table illustrates the error rate for each time.

Singular value decompostion algorithm

Process

Like stated above, real-time EMG signal is stored every 500ms. In this paragraph, another algorithm will be introduced to extract the feature of the EMG signal. Singular value is one of the characters of a matrix. The following theorems state the benefits of extracting features by singular value decomposition. Theorem 1: Stability of singular value A^(m*n),B^(m*n) ∈R^(m*n) The singular values of two matrix A and B are σ_1≥σ_2≥⋯≥σ_n and τ_1≥τ_2≥⋯≥τ_n respectively. Then it can be proved that： |σ_i-τ_i |≥|A-B|_2 i=1,2,…,n Therefore, when a matrix A has weak vibration, the change of its singular values is not larger than the Euclid norm. Which means singular values of a matrix is fairly stable. For signals that contain noise or trend, the feature matrix after SVD does not vary a lot. This character reduces the requirement of pre-treatment to sEMG signal and guarantees the accuracy of feature matching.

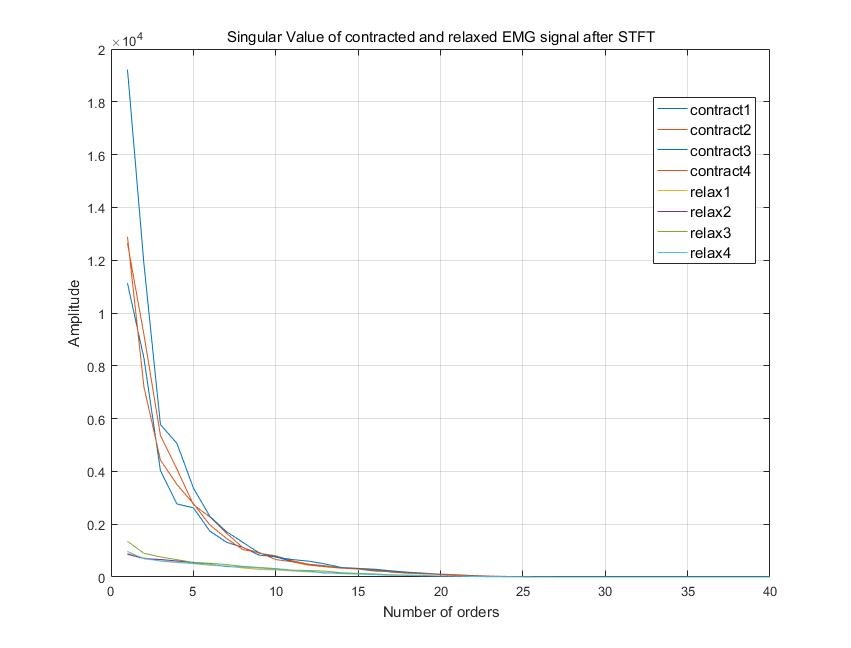
Theorem 2: Proportion invariance The singular values of matrix A^(m*n) areσ_1≥σ_2≥⋯≥σ_k. The singular values of matrix 〖α*A〗^(m*n) are〖σ_1〗^*≥〖σ_2〗^*≥⋯≥〖σ_k〗^*. Then |(-α∙A) (α∙A)^H-σ^(*2) I|=0 That is |AA^H-σ^(*2) I/α^2 |=0 So |α|(σ_1,σ_2,…,σ_k )=(〖σ_1〗^*,〖σ_2〗^*,…,〖σ_k〗^* ) Therefore, if the two matrixes are proportional, then their singular values are also proportional, and the proportion remains unchanged. This means normalization which is used to get rid of the influence of amplitude does not change the relative amplitude of singular values. It can be seen from the theorems above that singular value is an inherent character of a matrix, and it satisfies the requirement of SEMG feature extraction (stability and proportion invariance)[4]. It can be confirmed that singular value is an effective way to represent the feature of a matrix. The matrix that is used to represent the segment is the sEMG signal after STFT. By calculating the singular values of the complex matrix containing EMG segment after STFT and put them into the neural network, the project team was able to extract the feature of muscle state as the output. In this project, the signal after STFT was stored in a matrix, MATLAB code then calculated the singular value of the complex matrix. A plot of the singular values of an example EMG signal is shown below:

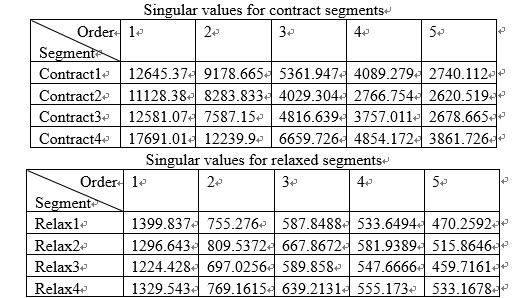
This figure shows that there is a significant difference between the singular values of contracted segments and relaxed segments. Contracted segments have larger singular values and relaxed ones have smaller singular values. Moreover, the plot of two different states of muscle follows their own trend, which makes it possible to separate two features using a BP neural network. It is clear that the singular value difference after the 5th order is too small compared to the first few orders. Therefore, all the small singular values of order 5 are omitted. In this project, the first five orders of the singular values were selected to be the feature singular values. These singular values will be put into the training data matrix. The training matrix has m rows and n columns, where m equals twice the length of training time in second (segment length = half a second) and n is the number of order taken into consideration, which is 5 in this project. All the rows for contracted EMG signal in the training matrix correspond to a [0 1] output in the neural network. The rest rows contain singular values from relaxed EMG segment and lead to a [0 0] output. In this way, the neural network is trained with the EMG signal generated by the same person’s same muscle at the same position, which will minimize the error caused by individual difference. All the training session is completed automatically without any manually set value.

The raw EMG signals used in this algorithm were recorded from a 24 years old healthy male’s left forearm. Through a 64-channel electrode and amplified with REFA amplifier. The singular values below are from contracted and relaxed segments of channel 1. The program asks the tester to contract the muscle for 8 seconds to record sEMG for contracted muscle. The segments are then analyzed by STFT and a new complex matrix will be created for the signal after STFT. After that, singular values of the complex matrix are put into the first 16 rows of the training feature matrix. After contraction training finishes, the tested will be asked to relax the muscle for 8 seconds to record sEMG for relaxed muscle. The Same procedure runs again and fills the training feature matrix with the singular values of relaxed segments. Four groups of singular values of contracted and relaxed segments are shown below respectively.

It can be seen that there is significant difference between the singular values of contracted and relaxed segments. Which means the separation of two states of muscle can be done well with the BP neural network. After training, the program starts real-time processing. The same procedure runs to calculate the singular values of the segments that are stored in the buffer. The singular values are then put into the neural network that was trained by the training feature in the preparation step. The output of the neural network is the state of the muscle in the period of 500ms. The results of muscle state are displayed on the screen.

Team members

Hanzhi Wang & Junyao Wang

Supervisiors

A. Prof. Mathias Baumert

Dr. Tien-fu Lu