Projects:2017s1-120 Hardware Realisation of the Unum 2.0 Number Format

Students: Thomas Chadwick, Reuben Sugars and Yuanli Chen

Supervisors: Sam Bahrami & Dr. Braden Phillips

Abstract

Unum 2 has been proposed as an alternative to IEEE 754 floating point arithmetic, a number format used extensively in computing today. It has been claimed that Unum 2 solves problems with floating point arithmetic, such as loss of accuracy due to repeated rounding. Furthermore it has been claimed that a hardware implementation of Unum 2 would be faster, use less area on a chip, and have higher accuracy than a floating point implementation. The purpose of our research is to test these claims by designing a hardware Unum 2 arithmetic unit and evaluating its performance in case study applications.

Motivation

Unum 2.0, (Universal Numbers 2.0, sometimes called Type 2 Unum) is a number system proposed for efficient and accurate binary operations on real numbers within a computer. The purpose of Unum 2.0 is to be a alternative way of processing real numbers in com- puter hardware, aimed at addressing limitations in current processing methods. The current standard for processing real numbers is IEEE 754, also known as floating-point. John Gustafson, who proposed Unum 2.0 in 2016 in the initial paper "A Radical Approach to Computation with Real Numbers" made the following claims about the benefits of Unum over floating-point including the following:

1) Extremely high energy efficiency and information per-bit

2) No penalty for decimal operations instead of binary

2) Rigorous bounds on answers

3) Unprecedented high speed up to some precision

4) Makes possible operating on arbitrary disconnected subsets of the real number line with the same speed as operating on a simple bound

The purpose of this project was to design and build a hardware implementation of Unum 2.0 in order to test the viability of the number system as an alternative to floating-point while verifying John Gustafson's claims about the benefits of the number system. Given the constant strive in hardware design to reduce power consumption while improving performance (precision and speed), the ability to use Unum 2.0 to further optimise hardware design processes, perhaps in place of an FPU ( oating-point unit) could be tremendously beneficial assuming that the claims of its benefits made are valid.

Research Question

Our research question was, “How does Unum 2.0 compare with IEEE 754 floating point arithmetic in terms of area on a chip, computational speed, and numerical accuracy?”

Research Approach

In order to test Unum 2.0 we have done the following:

1) Designed a software specification model of the Unum 2.0 implementation

2) Designed and implemented Unum 2.0 on an FPGA, and compared it with a similar bit length floating-point implementation

3) Used Genus Synthesis tools to explore a potential ASIC implementation of the Unum 2.0 unit.

Software Specification Model

Used to investigate precision and dynamic range properties of Unum 2.0. Unum gives you the ability to choose which numbers are represented exactly within your number system. This gives freedom to the designer, but also delegates responsibility. As the designer has this freedom, there is a significant requirement for look-up table space. This makes the design of hardware for a generic Unum system difficult to optimise.

In our software specification model we assessed how the restriction of lattice selection may serve to optimise the hardware, specifically how much look-up table space would be required. We looked at the functional generation of lattices, for example, having the exactly representable numbers follow a linear relationship. We found that lattices generated using an exponential function yielded the best results.

FPGA implementation

The FPGA used was on a Xilinx VC707 Evaluation board, and was a XC7VX485T chip.

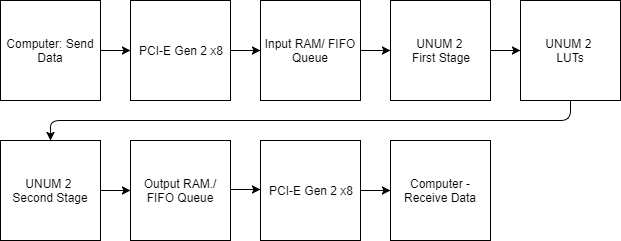
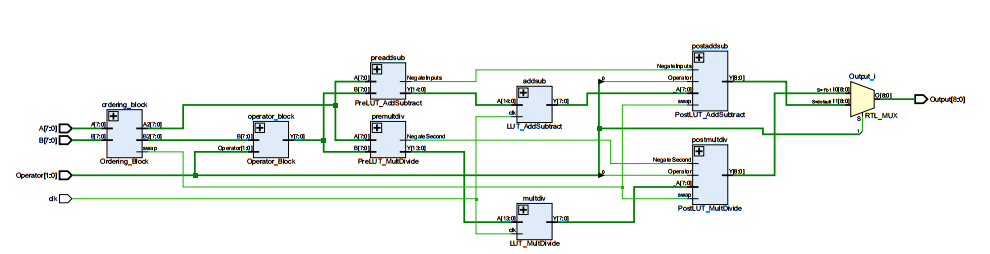
The FPGA implementation was able to send data from the computer to it, to do some Unum 2.0 calculations and send back. We implemented a 9-bit Unum, and compared it with a 9-bit custom precision float with the same implemented arithmetic operators. It was found that the space required on chip for the Unum 2.0 implementation grew exponentially for longer bit lengths so it was deemed that Unum 2.0 was better for shorter bit lengths.

It was found that the Unum 2.0 implementation wasn't able to run as fast as a floating-point unit, due to setup time requirements for the Block RAM (BRAM) used as LUTs causing a timing violation at lower frequencies. The BRAM also meant the system consumed more power than a floating-point implementation.

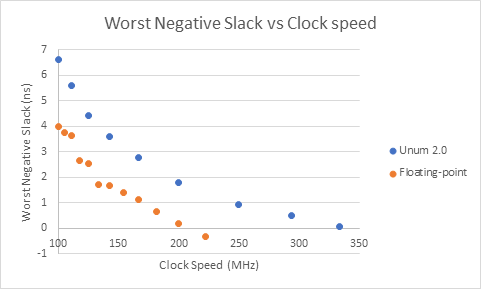
Worst Negative Slack (WNS) was used to measure whether timing requirements were met, if this goes negative then timing requirements are not met:

WNS stays positive up until higher clock speeds in the floating-point implementation

The area requirements/resource utilization by both floating-point and Unum 2.0 were compared also:

	Unum 2.0	Floating-point	Total Available
Slice LUTs	112	233	303600
Slice Registers	32	154	607200
Slice	49	92	75900
LUT as Logic	112	223	303600
LUT Flip-Flop Pairs	9	103	303600
Bonded IOB	28	42	42
BUFGCTRL	1	1	1
BRAM	12	0	1030

It can be observed that Unum, aside from its use of BRAM, uses less on board resources. However, this is for a 9-bit Unum, and increasing the bit length increases the BRAM use exponentially.

ASIC Design Exploration

Genus synthesis tools were used with the FreePDK45 technology library (a technology library free to use for academic purposes) to investigate an ASIC implementation. It was found that the ASIC implementation was capable of driving much higher clock speeds at lower power consumption than the FPGA implementation.

Conclusions

1) Difficult to pick u-lattices (the set of numbers that are represented exactly by Unums) that provide good precision and dynamic range properties for general purpose use.

2) Unum area requirements grow exponentially with bit length, making it only suitable for low bit length applications.

3) Area is less than that of floating-point at shorter bit lengths

4) Was unable to reproduce proposed speed or on-chip power advantages over floating-point, due to the BRAM memory used to store LUTs. These issues could potentially be resolved in the custom ASIC solution.

Future Work

1) Investigate and implement applications that may benefit from short word lengths and lower precision.

2) Look into additional ways to reduce LUT size, perhaps with loss of precision, but greatly reducing on chip area.

3) Investigate ASIC design in further detail, including effect of LUT space on chip area and costs associated.

References

J. Gustafson, "A Radical Approach to Computation with Real Numbers" \emph{Supercomputing Frontiers and Innovations}, vol. 32, no. 2, 2016

J. Gustafson, "A Radical Approach to Computation with Real Numbers (Slide Presentation)" April 23, 2016; [1]

Prof. W. Kahan "Prof. W. Kahan's Comments on SORN Arithmetic" July 15, 2016; [2]

M. Guthaus, J. Stein, S. Ataei, B. Chen, B. Wu and M. Sarwar, "OpenRAM: an open-source memory compiler", ICCAD '16, no. 93, 2016

M. Jacobsen, D. Richmond, M. Hogains, and R. Kastner, "RIFFA 2.1: A reusable integration framework for FPGA accelerators." ACM Transactions on Reconfigurable Technology and Systems (TRETS), September 2015

D. Goldberg "What Every Computer Scientist Should Know About Floating Point Arithmetic" \emph{ACM Computing Surveys}, vol. 23, no. 1, March 1991

Xilinx "Block Memory Generator v8.2" Product Guide, April 1, 2015; [3]

Xilinx "LogiCORE IP Floating-Point Operator v7.0" Product Guide, April 2, 2014; [4]

Xilinx "Distributed Memory Generator v8.0" Product Guide, November 18, 2015; [5]

Xilinx "Design Analysis and Closure Techniques" Vivado Design Suite User Guide, August 20, 2012; [6]

Xilinx "7 Series FPGAs Data Sheet: Overview" XC7VX485T Data Sheet, August 1, 2017; [7]