Projects:2018s1-107 Evolution of Spiking Neural Networks for UAV Control

Group members

Lachlan Bateman, Paul Elson, Matthew Astachnowicz and Alexander Makarowsky

Supervisors

Dr Hong Gunn Chew, Dr Braden Phillips and sponsor Dr David Howard (CSIRO)

Introduction

Every unmanned aerial vehicle (UAV) contains a flight controller, which calculate roll, pitch, yaw and thrust signals from the UAV's current position and its desired position. A flight controller is often used by higher-level control structures in autonomous behaviours such as path planning and object avoidance.

System diagram of a flight controller

This project investigates the use of a biologically-inspired computational model known as a spiking neural network (SNN) to perform UAV flight control. Like conventional artificial neural networks, an SNN consists of a network of small processing nodes called biological neurons. The key difference between spiking and conventional artificial neural networks lies in the inter-neuron signalling: spiking neurons communicate through precisely timed binary 'spikes' as opposed to regularly propagated continuous values. The processing power of a spiking neural network is believed to be significantly greater than that of conventional artificial neural networks when comparing networks of similar size .

Spikes into a neuron excite the neuron's membrane voltage. If excited sufficiently, the neuron will produce an output spike

Motivation

Improving the performance of quadcopter flight controllers facilitates UAV applications in an ever-wider range of challenging environments, such as inside mine shafts. As each controller must be adjusted or 'tuned' to a given system, reducing the time required to tune a controller is also of enormous importance to deployment capability. High performance or fast-tuning flight controllers are of enormous military and civilian interest.

Proportional-integral-differential (PID) flight control schemes see widespread use for UAV flight control . While PID-based control schemes are generally easy to tune and implement, they are fundamentally linear control schemes. As quadcopter and hexacopter system dynamics are nonlinear, flight control has been shown to benefit from nonlinear control schemes which can compensate for nonlinearities in the underlying plant .

A nonlinear system of differential equations governs the relationship between a spiking neuron’s internal state, its inputs and its outputs. The nonlinearity of SNNs produces nonlinear functional approximation, and hence potentiates improved flight control performance in comparison to linear PID architectures. One such potential area of improvement is a common tradeoff between disturbance rejection and set-point tracking.

The nonlinearity of SNNs however comes at a cost: conventional artificial neural networks training algorithms cannot be directly applied to optimise the control network. This research uses a family of biologically-inspired search algorithms known as evolutionary algorithms (EAs) to develop high performance controllers.

Position and Speed Control of a DC Motor

Flight control of a quadcopter is a nonlinear, multiple-input multiple-output control problem. To build towards this goal, the position and speed control of a DC motor were adopted as preliminary stepping-stone problems, as they represent highly linear single-input single-output problems.

Laplace-domain representation of the transform between the voltage applied to a DC motor and its speed

Spiking neural network controllers were developed both for simulated motors as well as for a physical DC motor. As both position and speed control are linear problems, it is possible to easily compare spiking neural network control performance to a variety of conventional techniques, such as optimal feedback controllers. The DC motor control problems also provide a great deal of insight into the level of accuracy required in simulation before tuned controllers can be readily transferred to hardware.

Physical DC motor embedded platform

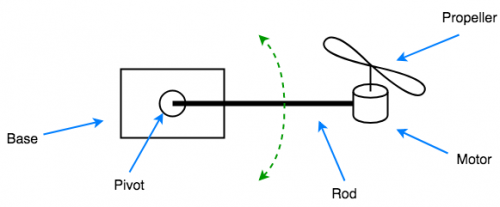
Angular Control of a 1D Propeller Arm

To progress from a linear single-input single-output (SISO) problem to a nonlinear SISO problem, a one-dimensional propeller arm was constructed. The one-dimensional arm resembles one component of a full UAV flight controller, namely the component which controls a UAV's height. The one-dimensional arm is also a highly nonlinear, as the dynamics of the plant change substantially with the angle of the arm.

System diagram of the 1D arm

The system was modelled in software to provide an easily-accessible platform for evolution experiments. The software model was improved iteratively until the solutions evolved in software were sufficiently transferable to the hardware system.

Physical 1D arm in safety enclosure

Embedded Platform

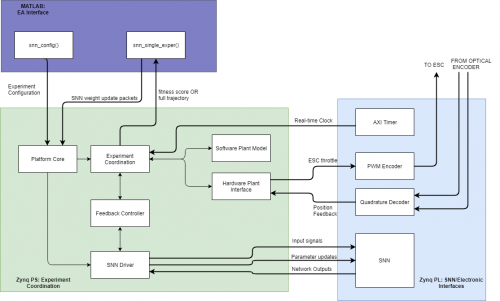
For both the motor control and 1D arm control experiments, a significant quantity of development work was required to integrate sensors, actuators and log data between experiments and controller evaluations. A Zynq combined FPGA/microprocessor was used throughout the project to perform such tasks. The Zynq also also facilitated the parallelisation of controller evaluations in software, which significantly reduced the time required to evolve high-performing controllers.

The timing precision of at which any SNN was simulated as well as any underlying fixed-point precision were found to both greatly affect controller performance. Understanding how each of these parameters affected the signal precision in terms of rounding proved critical to evolving high-performing controllers.

Signal flow diagram for the 1D arm embedded platform. Note that the optical encoder measures the arm's angle, while an electronic speed controller (ESC) drives the propeller motor

Results

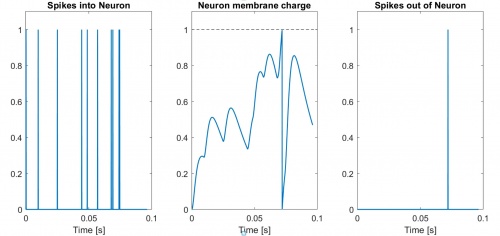
Early SNN control experiments on both physical and simulated DC motors led to performance that was quite poor when compared to conventional control techniques, such as well-tuned PID tuned or optimal control approaches. An example of an early manually-tuned speed control network is shown below.

Response of a simulated DC motor to variations in speed set point under control of a 4-neuron SNN

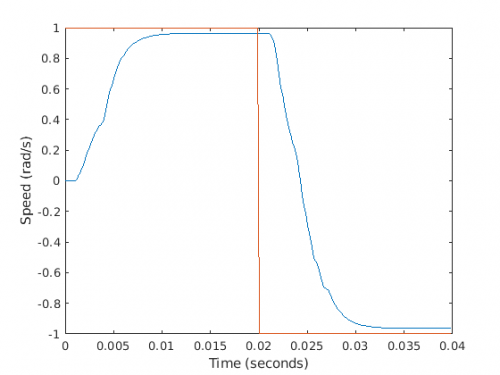
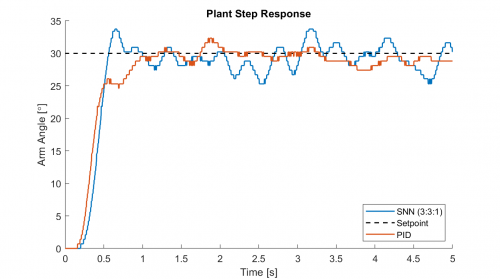
The angle of the 1D arm in response to a 30 degree change in setpoint both under PID control and when controlled by a small-scale spiking neural network is shown below. The performance of the SNN controller was found to depend substantially upon the simulation frequency and the level of fixed-point precision used in the embedded platform.

Comparison of control responses for the 1D arm

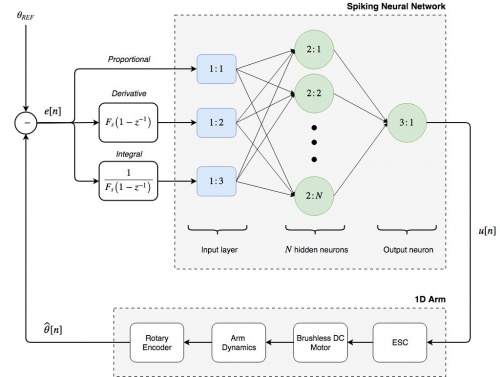
A system diagram of one of high-performance control network topologies is shown below.

System diagram of a viable small-scale SNN 1D arm controller

Conclusions

To the best of our knowledge, closed-loop control of the physical 1D arm represents the first time that a research group has successfully applied spiking neural networks to an unstable physical plant outside of simulation.

For control applications, SNNs much be simulated with a very high degree of timing precision to produce acceptable performance in terms of closed-loop stability and classical control metrics such as steady-state error. High simulation frequencies in turn necessitate the use of dedicated hardware, such as FPGAs, to produce the signal precision required to produce high-quality control responses.

Evolutionary algorithms have so far proven incapable of generating small-scale SNNs (<10 neurons) which are capable of controlling unstable systems, such as the 1D arm, which when provided solely with the control variable error. Providing small-scale SNNs with explicitly calculated error derivative terms does however result result in system stabilisation and effective plant control. Several recent research publications have also required a derivative term to stabilise simulated systems.

Future Research Opportunities

The next stage for this research is the transition from single-input single-output (SISO) control problems to larger scale multiple-input multiple-output control problems, such as the flight control of a quadcopter. The size of the control network required will likely be significantly larger than that of the SISO controllers.

Flight control will likely be first explored in simulation, on a suitable platform such as QrSim. Transitioning to the SNN control of a UAV in hardware will represent a significantly larger challenge, as there are several aspects of the full control system, such as gyroscopes for state estimation, which will require substantial effort to integrate into a full system.