Projects:2018s1-128 Software Tool for Fitting Statistical Models to Sea Clutter Data
Contents
Supervisors
Dr.Brian Ng Dr.Luke Rosenberg
Members
Chengjun Shao Aaron Boyall
Introduction
This project will automatically fit a variety of amplitude distributions to real sea-clutter data and present to the user the best model. A Graphical User Interface (written in MATLAB) would be useful to visualize the fitting results. The models to be considered may include classical models such as the Rayleigh, Gamma, Weibull, Lognormal as well as the popular compound distributions, K, Pareto, 3MD, Fisher and their variants. The 'best' model fit should be based on a number of criteria such as the Chi-Squared or Kolmogorov Smirnoff statistical tests, with options to focus on the distribution tail.
Motivation
The Australian Defence Science and Technology (DST) Group models observed sea clutter data in MATLAB using statistical distributions and part of the distributions already have MATLAB implementations. The DST group wants a simple, easy-to-use tool, featuring a graphical user interface, that will allow them to estimate the parameters of raw radar data, and compare how well each of the distributions fits the data set. They also require the given distributions to each have a written report on their parameters and how they were calculated.
Significance
The project has benefits that it develops an accurate model analysis on sea clutter data, which is very significant to DST group and pose numerous benefits to maritime radar in terms of efficiency and functionality whereas radar is essential for detecting sea craft in Australia’s maritime territory and prevent illegal activity with Australia’s waters such as illegal fishery, illegal immigrants.
Technical background
Most of maritime radar will identify the target by analyzing the return signal. The received signal by maritime radar mainly consist of three parts: noise, clutter and true target. The noise and clutter are the unwanted signal parts whereas the true target signal part is desired signal part.
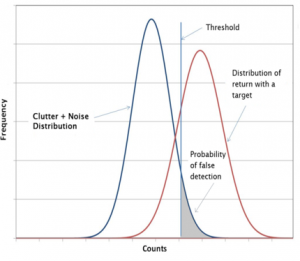
As is shown in the graph, the Y-axis represents the frequency and X-axis represents the counts of responding frequency. The area under the red curve to the right of the threshold shows the possibility we detect the target signal. The area under blue curve to the left threshold shows the possibility we detect the noise. The area under the blue curve to the right threshold shows the possibility we make a false detection, which will affect the false alarm. The graph which is shown above can also reflect the value of Signal-to-noise ratio (SNR). Signal-to-noise ratio (SNR) is a measure used in radar analysis that compares the level of a desired signal to the level of background noise. If the ratio of the signal to the noise get higher, the red curve will shift right, then the more area is under red curve to the right of the threshold, which means the probability of detection will get greater.
Error metrics set
These metrics measure the different between the model fit and the data. The difference analysis between the measured clutter amplitude and corresponding distribution model can be made by the Kolmogorov-Smirnov (K-S), Chi-squared test, Bhattacharyya metric and threshold error.
Kolmogorov-Smirnov (K-S) test
Kolmogorov–Smirnov test (KS test) is a test of one-dimensional probability distributions. According to the number of samples, the KS test can be identified as one sample KS test and two sample KS tests. Samples are used to make a comparison with a reference probability distribution in order to judge the goodness of best fit.
The main purpose of KS test is to compare the difference between the cumulative probability of the actual frequency and the theoretical frequency, find the maximum distance D, and determine whether the actual frequency distribution obeys the theoretical frequency distribution according to the D value.
In MATLAB, we can use [h,p,ksstat,cv] = kstest(___) to get the Hypothesis test result h, p, test statistic of the hypothesis test ksstat and Critical value cv. h represents the result of Hypothesis test, which is 1 or 0.
Situation 1: h = 1, representing the rejection of the null hypothesis. Situation 2: h = 0, representing a failure to reject the null hypothesis. p is a scalar value from 0 to 1, which is able to reflect the probability of observing a test statistic as extreme as the observed value under the null hypothesis. ksstat represents the test statistics, which is a non-negative scalar. cv represents the critical value, which is a non-negative scalar.
Chi-squared test
A chi-squared test is a hypothesis test where the sampling distribution of the test statistic is a chi-squared distribution when the null hypothesis is true. The most basic idea of the ‘chi-square test’ is to use observational differences between actual and theoretical values to determine whether the theory is correct or not. The specific steps are: firstly, assume that the two variable models are consistent, and then observe the difference between actual values and theoretical values, if the deviation is small enough, we think that the two models are indeed the same. If the deviation is greater than a certain degree and exceeds its critical value, we think that the two are actually different. In MATLAB, the chi-square test determines if a data sample comes from a specified probability distribution, with parameters estimated from the data.
The Oi and Ei represent the observed counts and expected counts respectively for the bins where stored the grouped data. The chi-square test statistic will be computed based on the hypothesized distribution. The test statistic will take on an approximate chi-square distribution when the counts are large enough.
In MATLAB, we can use [h,p,stats] = chi2gof(___) to get the Hypothesis test result h, p and test statistic stat. The representation of h,p is same as KS test while the meaning of stats is totally different from the KS test. Stats represent the test statistics here, which is a structure including multiple parameters about bins.
Bhattacharyya metric
In statistical distribution, the Bhattacharyya metric is used to measure the similarity between the theoretical and the actual distribution models by comparing their Bhattacharyya distance and coefficient.
Threshold error
The reason why we try to make the PDF model more accurate is to improve the radar performance and target detection ability. The interference part that including the noise and clutter is always unwanted for detection. In order to distinguish the signal part between target plus interference and the interference itself at false alarm rate, it is necessary to set and find the most accurate threshold to make analysis. Generally, we set log-transform(10 log 10) as Y-axis when we make analysis on threshold, the reason to log-transform the data is that upregulated or downregulated data (compared to a control sample) will not be normally distributed, which can be problematic if using a parametric statistical test (KS test). By log transforming the data, upregulated and downregulated expression data can then have a similar scale of changes, which is helpful to make intuitive analysis.
In this project, the probability of false alarm is the complementary CDF (CCDF = 1- CDF). Threshold error is determined by first calculating the CCDF for both the empirical data and fitted data, where the CCDF displays which percentile of the data lies below a certain value. The threshold error is the absolute difference between the two results at a fixed CCDF (complimentary cumulative distribution function) value.
Monte-Carlo simulation
Monte Carlo simulation is a mean to perform risk analysis by building models of possible results by substituting a range of values—a probability distribution—for any factor that has inherent uncertainty. It then calculates results over and over, each time using a different set of random values from the probability functions. Depending upon the number of uncertainties and the ranges specified for them, a Monte Carlo simulation could involve thousands or tens of thousands of recalculations before it is complete. Monte Carlo simulation produces distributions of all possible outcome values. The general steps to design Monte-Carlo simulation:
Define a domain of possible inputs
Generate inputs randomly from a probability distribution over the domain
Perform a deterministic computation on the inputs
Aggregate the results